Pseudo Johnson-Neyman Probing

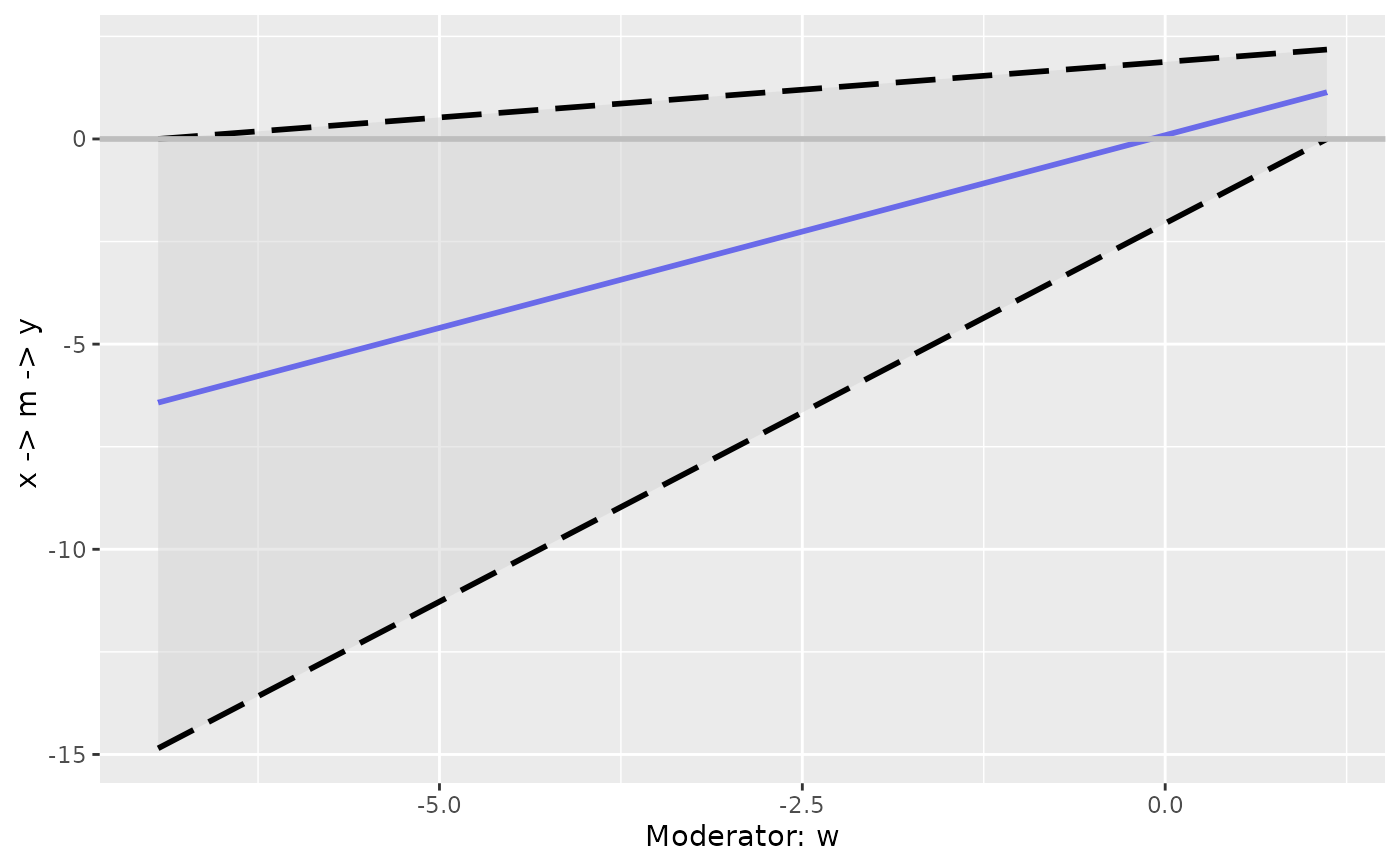
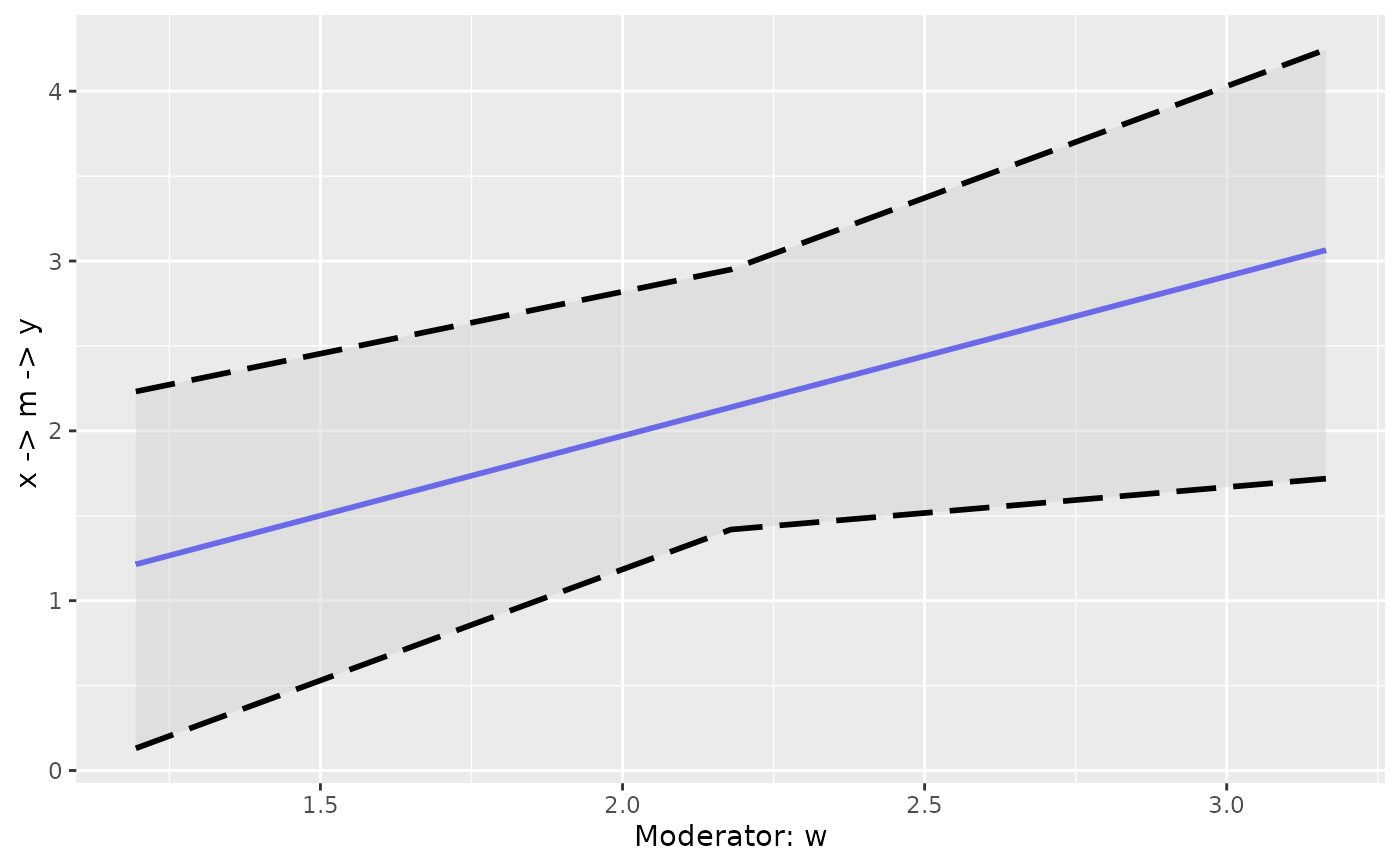
Use the pseudo Johnson-Neyman approach (Hayes, 2022) to find the range of values of a moderator in which the conditional effect is not significant.

Usage

pseudo_johnson_neyman(
  object = NULL,
  w_lower = NULL,
  w_upper = NULL,
  optimize_method = c("uniroot", "optimize"),
  extendInt = c("no", "yes", "downX", "upX"),
  tol = .Machine$double.eps^0.25,
  level = 0.95
)

johnson_neyman(
  object = NULL,
  w_lower = NULL,
  w_upper = NULL,
  optimize_method = c("uniroot", "optimize"),
  extendInt = c("no", "yes", "downX", "upX"),
  tol = .Machine$double.eps^0.25,
  level = 0.95
)

# S3 method for class 'pseudo_johnson_neyman'
print(x, digits = 3, ...)

Arguments

object: A cond_indirect_effects-class object, which is the output of cond_indirect_effects().
w_lower: The smallest value of the moderator when doing the search. If set to NULL, the default, it will be 10 standard deviations below mean, which should be small enough.
w_upper: The largest value of the moderator when doing the search. If set to NULL, the default, it will be 10 standard deviations above mean, which should be large enough.
optimize_method: The optimization method to be used. Either "uniroot" (the default) or "optimize", corresponding to stats::uniroot() and stats::optimize(), respectively.
extendInt: Used by stats::uniroot(). If "no", then search will be conducted strictly within c(w_lower, w_upper). Otherwise, the range is extended based on this argument if the solution is not found. Please refer to stats::uniroot() for details.
tol: The tolerance level used by both stats::uniroot() and stats::optimize().
level: The level of confidence of the confidence level. One minus this level is the level of significance. Default is .95, equivalent to a level of significance of .05.
x: The output of pseudo_johnson_neyman().
digits: Number of digits to display. Default is 3.
...: Other arguments. Not used.

Value

A list of the class pseudo_johnson_neyman (with a print method, print.pseudo_johnson_neyman()). It has these major elements:

cond_effects: An output of cond_indirect_effects() for the two levels of the moderator found.
w_min_valid: Logical. If TRUE, the conditional effect is just significant at the lower level of the moderator found, and so is significant below this point. If FALSE, then the lower level of the moderator found is just the lower bound of the range searched, that is, w_lower.
w_max_valid: Logical. If TRUE, the conditional effect is just significant at the higher level of the moderator found, and so is significant above this point. If FALSE, then the higher level of the moderator found is just the upper bound of the range searched, that is, w_upper.

Details

This function uses the pseudo Johnson-Neyman approach proposed by Hayes (2022) to find the values of a moderator at which a conditional effect is "nearly just significant" based on confidence interval. If an effect is moderated, there will be two such points (though one can be very large or small) forming a range. The conditional effect is not significant within this range, and significant outside this range, based on the confidence interval.

This function receives the output of cond_indirect_effects() and search for, within a specific range, the two values of the moderator at which the conditional effect is "nearly just significant", that is, the confidence interval "nearly touches" zero.

Note that numerical method is used to find the points. Therefore, strictly speaking, the effects at the end points are still either significant or not significant, even if the confidence limit is very close to zero.

Though numerical method is used, if the test is conducted using the standard error (see below), the result is equivalent to the (true) Johnson-Neyman (1936) probing. The function johnson_neyman() is just an alias to pseudo_johnson_neyman(), with the name consistent with what it does in this special case.

Supported Methods

This function supports models fitted by lm(), lavaan::sem(), and semTools::sem.mi(). This function also supports both bootstrapping and Monte Carlo confidence intervals. It also supports conditional direct paths (no mediator) and conditional indirect paths (with one or more mediator), with x and/or y standardized.

Requirements

To be eligible for using this function, one of these conditions must be met:

One form of confidence intervals (e.g, bootstrapping or Monte Carlo) must has been requested (e.g., setting boot_ci = TRUE or mc_ci = TRUE) when calling cond_indirect_effects().
Tests can be done using stored standard errors: A path with no mediator and both the x- and y-variables are not standardized.

For pre-computed confidence intervals, the confidence level of the confidence intervals adopted when calling cond_indirect_effects() will be used by this function.

For tests conducted by standard errors, the argument level is used to control the level of significance.

Possible failures

Even if a path has only one moderator, it is possible that no solution, or more than one solution, is/are found if the relation between this moderator and the conditional effect is not linear.

Solution may also be not found if the conditional effect is significant over a wide range of value of the moderator.

It is advised to use plot_effect_vs_w() to examine the relation between the effect and the moderator first before calling this function.

Speed

Note that, for conditional indirect effects, the search can be slow because the confidence interval needs to be recomputed for each new value of the moderator.

Limitations

This function currently only supports a path with only one moderator,
This function does not yet support multigroup models.

Methods (by generic)

print(pseudo_johnson_neyman): Print method for output of pseudo_johnson_neyman().

References

Johnson, P. O., & Neyman, J. (1936). Test of certain linear hypotheses and their application to some educational problems. Statistical Research Memoirs, 1, 57–93.

Hayes, A. F. (2022). Introduction to mediation, moderation, and conditional process analysis: A regression-based approach (Third edition). The Guilford Press.

Examples


library(lavaan)

dat <- data_med_mod_a
dat$wx <- dat$x * dat$w
mod <-
"
m ~ x + w + wx
y ~ m + x
"
fit <- sem(mod, dat)

# In real research, R should be 2000 or even 5000
# In real research, no need to set parallel and progress to FALSE
# Parallel processing is enabled by default and
# progress is displayed by default.
boot_out <- do_boot(fit,
                    R = 50,
                    seed = 4314,
                    parallel = FALSE,
                    progress = FALSE)
out <- cond_indirect_effects(x = "x", y = "y", m = "m",
                             wlevels = "w",
                             fit = fit,
                             boot_ci = TRUE,
                             boot_out = boot_out)

# Visualize the relation first
plot_effect_vs_w(out)


out_jn <- pseudo_johnson_neyman(out)
out_jn
#> 
#> == Pseudo Johnson-Neyman Probing ==
#> 
#> The conditional effect is not significant when w is greater than -6.938
#> and less than 1.114, and is significant when w is outside this range,
#> at 0.05 level of significance.
#> - On 'Sig': A conditional effect at the bound of the range may be
#> marked as significant or not significant. However, it can be treated as
#> 'just significant' if its confidence interval practically 'touches'
#> zero.
#> 
#> == Conditional indirect effects ==
#> 
#>  Path: x -> m -> y
#>  Conditional on moderator(s): w
#>  Moderator(s) represented by: w
#> 
#>    [w]    (w)    ind   CI.lo CI.hi Sig    m~x   y~m
#> 1 High  1.114  1.139   0.000 2.179 Sig  1.179 0.966
#> 2 Low  -6.938 -6.425 -14.850 0.000     -6.650 0.966
#> 
#>  - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#>    nonparametric bootstrapping with 50 samples.
#>  - The 'ind' column shows the conditional indirect effects.
#>  - ‘m~x’,‘y~m’ is/are the path coefficient(s) along the path conditional
#>    on the moderator(s).
#> 

# Plot the range
plot_effect_vs_w(out_jn$cond_effects)