manymome

Introduction

This article is a brief illustration of how main functions from the package manymome (Cheung & Cheung, 2023) can be used in some typical cases. It assumes that readers have basic understanding of mediation, moderation, moderated mediation, structural equation modeling (SEM), and bootstrapping.

Workflow

The use of manymome adopts a two-stage workflow:

Stage 1: Fit the model
- This can be done by SEM (using lavaan::sem()) or a series of regression (using lm()).
- When lavaan::sem() is used, no need to label any parameters or denote any variables as the predictors, mediators, moderators, or outcome variables for computing indirect effects or conditional indirect effects. Stage 2 will take care of this.
Stage 2: Compute the indirect effects and conditional indirect effects
- This can be done along nearly any path in the model for any levels of the moderators.
- Just specify the start (x), the mediator(s) (m, if any), and the end (y) for indirect effects. The functions will find the coefficients automatically.
- If a path has one or more moderators, conditional indirect effects can be computed. Product terms will be identified automatically.
- The levels of the moderators can be decided in this stage and can be changed as often as needed.

Bootstrapping confidence intervals: All main functions support bootstrap confidence intervals for the effects. Bootstrapping can done in Stage 1 (e.g., by lavaan::sem() using se = "boot") or in Stage 2 in the first call to the main functions, and only needs to be conducted once. Alternatively, do_boot() can be use (see vignette("do_boot")). The bootstrap estimates can be reused by most main functions of manymome for any path and any level of the moderators.

Monte Carlo confidence intervals: Initial support for Monte Carlo confidence interval has been added to all main functions for the effects in a model fitted by lavaan::sem(). The recommended workflow is to use do_mc() to generate the simulated sampling estimates. The simulated estimates can be reused by most main functions of manymome for any path and any level of the moderators. To keep the length of this vignette short, it only covers bootstrapping confidence intervals. Please see vignette("do_mc") for an illustration on how to form Monte Carlo confidence intervals.

Standardized effects: All main functions in Stage 2 support standardized effects and form their bootstrap confidence interval correctly (Cheung, 2009; Friedrich, 1982). No need to standardize the variables in advance in Stage 1, even for paths with moderators.

What Will Be Covered In This Get-Started Article

Use cond_indirect_effects() to compute conditional indirect effects, with bootstrap confidence intervals.
Use indirect_effect() to compute an indirect effect, with bootstrap confidence interval.
Use + and - to compute a function of effects, such as total indirect effects or total effects.
Use do_boot() to generate bootstrap estimates for cond_indirect_effects(), indirect_effect(), and some other functions in manymome.
Use index_of_mome() and index_of_momome() to compute the index of moderated mediation and the index of moderated moderated mediation, respectively, with bootstrap confidence intervals.
Compute standardized conditional indirect effects and standardized indirect effect using cond_indirect_effects() and indirect_effect(), respectively.

Moderated Mediation by SEM using `lavaan`

This is the sample data set comes with the package:

library(manymome)
dat <- data_med_mod_ab
print(head(dat), digits = 3)
#>       x   w1   w2    m    y    c1   c2
#> 1  9.27 4.97 2.66 3.46 8.80  9.26 3.14
#> 2 10.79 4.13 3.33 4.05 7.37 10.71 5.80
#> 3 11.10 5.91 3.32 4.04 8.24 10.60 5.45
#> 4  9.53 4.78 2.32 3.54 8.37  9.22 3.83
#> 5 10.00 4.38 2.95 4.65 8.39  9.58 4.26
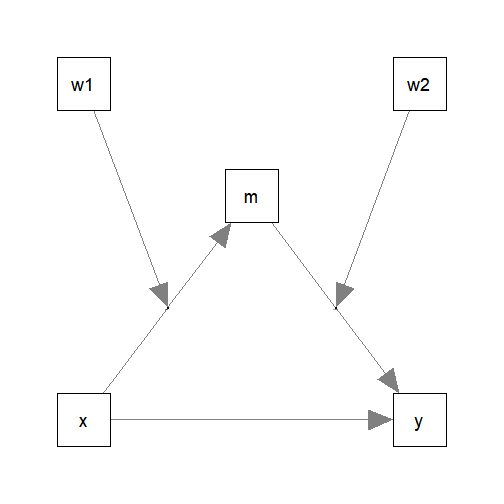
#> 6 12.25 5.81 4.04 4.73 9.65  9.51 4.01

Suppose this is the model being fitted:

plot of chunk manymome_draw_model

The models are intended to be simple enough for illustration but complicated enough to show the flexibility of manymome. More complicated models are also supported, discussed later.

Fitting the Model

The model fitted above is a moderated mediation model with

a mediation path x -> m -> y, and
two moderators:
- x -> m moderated by w1
- m -> y moderated by w2.

The effects of interest are the conditional indirect effects: the indirect effects

from x to y
through m
for different levels of w1 and w2.

cond_indirect_effects() can estimate these effects in the model fitted by lavaan::sem(). There is no need to label any path coefficients or define any user parameters (but users can, if so desired; they have no impact on the functions in manymome). To illustrate a more realistic scenario, two control variables, c1 and c2, are also included.

library(lavaan)
# Form the product terms
dat$w1x <- dat$w1 * dat$x
dat$w2m <- dat$w2 * dat$m
mod <-
"
m ~ x + w1 + w1x + c1 + c2
y ~ m + w2 + w2m + x + c1 + c2
# Covariances of the error term of m with w2m and w2
m ~~ w2m + w2
# Covariance between other variables
# They need to be added due to the covariances added above
# See Kwan and Chan (2018) and Miles et al. (2015)
w2m ~~ w2 + x + w1 + w1x + c1 + c2
w2  ~~ x + w1 + w1x + c1 + c2
x   ~~ w1 + w1x + c1 + c2
w1  ~~ w1x + c1 + c2
w1x ~~ c1 + c2
c1  ~~ c2
"
fit <- sem(model = mod,
           data = dat,
           fixed.x = FALSE,
           estimator = "MLR")

MLR is used to take into account probable nonnormality due to the product terms. fixed.x = FALSE is used to allow the predictors to be random variables. This is usually necessary when the values of the predictor are also sampled from the populations, and so their standard deviations are sample statistics.

These are the parameter estimates of the paths:

parameterEstimates(fit)[parameterEstimates(fit)$op == "~", ]
#>    lhs op rhs    est    se      z pvalue ci.lower ci.upper
#> 1    m  ~   x -0.663 0.533 -1.244  0.213   -1.707    0.381
#> 2    m  ~  w1 -2.290 1.010 -2.267  0.023   -4.269   -0.310
#> 3    m  ~ w1x  0.204 0.101  2.023  0.043    0.006    0.401
#> 4    m  ~  c1 -0.020 0.079 -0.251  0.801   -0.175    0.135
#> 5    m  ~  c2 -0.130 0.090 -1.444  0.149   -0.306    0.046
#> 6    y  ~   m -0.153 0.248 -0.616  0.538   -0.638    0.333
#> 7    y  ~  w2 -0.921 0.401 -2.300  0.021   -1.706   -0.136
#> 8    y  ~ w2m  0.204 0.079  2.579  0.010    0.049    0.359
#> 9    y  ~   x  0.056 0.086  0.653  0.514   -0.113    0.225
#> 10   y  ~  c1 -0.102 0.081 -1.261  0.207   -0.261    0.056
#> 11   y  ~  c2 -0.108 0.087 -1.249  0.212   -0.279    0.062

The moderation effects of both w1 and w2 are significant. The indirect effect from x to y through m depends on the level of w1 and w2.

Conditional Indirect Effects

To form bootstrap confidence intervals, bootstrapping needs to be done. There are several ways to do this. We first illustrate using do_boot().

Do Bootstrapping (Once)

Using do_boot() instead of setting se to "boot" when calling lavaan::sem() allows users to use other method for standard errors and confidence intervals for other parameters, such as the various types of robust standard errors provided by lavaan::sem().

The function do_boot() is used to generate and store bootstrap estimates as well as implied variances of variables, which are needed to estimate standardized effects.

fit_boot <- do_boot(fit = fit,
                    R = 500,
                    seed = 53253,
                    ncores = 1)

These are the major arguments:

fit: The output of lavaan::sem().
R: The number of bootstrap samples, which should be 2000 or even 5000 in real research. R is set to 500 here just for illustration.
seed: The seed to reproduce the results.
ncores: The number of processes in parallel processing. The default number is the number of detected physical cores minus 1. Can be omitted in real studies. Set to 1 here for illustration.

By default, parallel processing is used, and so the results are reproducible with the same seed only if the number of processes is the same. See do_boot() for other options and vignette("do_boot") on the output of do_boot().

The output, fit_boot in this case, can then be used for all subsequent analyses on this model.

Estimate Conditional Indirect Effects

To compute conditional indirect effects and form bootstrap confidence intervals, we can use cond_indirect_effects().

out_cond <- cond_indirect_effects(wlevels =c("w1", "w2"),
                                  x = "x",
                                  y = "y",
                                  m = "m",
                                  fit = fit,
                                  boot_ci = TRUE,
                                  boot_out = fit_boot)

These are the major arguments:

wlevels: The vector of the names of the moderators. Order does not matter. If the default levels are not suitable, custom levels can be created by functions like mod_levels() and merge_mod_levels() (see vignette("mod_levels")).
x: The name of the predictor.
y: The name of the outcome variable.
m: The name of the mediator, or a vector of names if the path has more than one mediator (see this example).
fit: The output of lavaan::sem().
boot_ci: Set to TRUE to request bootstrap confidence intervals. Default is FALSE.
boot_out: The pregenerated bootstrap estimates generated by do_boot() or previous call to cond_indirect_effects() or indirect_effect().

This is the output:

out_cond
#> 
#> == Conditional indirect effects ==
#> 
#>  Path: x -> m -> y
#>  Conditional on moderator(s): w1, w2
#>  Moderator(s) represented by: w1, w2
#> 
#>      [w1]    [w2]  (w1)  (w2)   ind  CI.lo CI.hi Sig   m~x   y~m
#> 1 M+1.0SD M+1.0SD 6.173 4.040 0.399  0.139 0.705 Sig 0.596 0.671
#> 2 M+1.0SD M-1.0SD 6.173 2.055 0.158 -0.025 0.381     0.596 0.266
#> 3 M-1.0SD M+1.0SD 4.038 4.040 0.107 -0.148 0.358     0.160 0.671
#> 4 M-1.0SD M-1.0SD 4.038 2.055 0.043 -0.062 0.191     0.160 0.266
#> 
#>  - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#>    nonparametric bootstrapping with 500 samples.
#>  - The 'ind' column shows the conditional indirect effects.
#>  - 'm~x','y~m' is/are the path coefficient(s) along the path conditional
#>    on the moderator(s).

For two or more moderators, the default levels for numeric moderators are one standard deviation (SD) below mean and one SD above mean. For two moderators, there are four combinations.

As shown above, among these four sets of levels, the indirect effect from x to y through m is significant only when both w1 and w2 are one SD above their means. The indirect effect at these levels of w1 and w2 are 0.399, with 95% bootstrap confidence interval [0.139, 0.705].

The function cond_indirect_effects(), as well as other functions described below, also supports bias-corrected (BC) confidence interval, which can be requested by adding boot_type = "bc" to the call. However, authors in some recent work do not advocate this method (e.g., Falk & Biesanz, 2015; Hayes, 2022; Tofighi & Kelley, 2020). Therefore, this option is provided merely for research purpose.

Examine the Effect at a Particular Set of Levels of the Moderators

To learn more about the conditional effect for one combination of the levels of the moderators, get_one_cond_indirect_effect() can be used, with the first argument the output of cond_indirect_effects() and the second argument the row number. For example, this shows the details on the computation of the indirect effect when both w1 and w2 are one SD above their means (row 1):

get_one_cond_indirect_effect(out_cond, 1)
#> 
#> == Conditional Indirect Effect   ==
#>                                                     
#>  Path:                        x -> m -> y           
#>  Moderators:                  w1, w2                
#>  Conditional Indirect Effect: 0.399                 
#>  95.0% Bootstrap CI:          [0.139 to 0.705]      
#>  When:                        w1 = 6.173, w2 = 4.040
#> 
#> Computation Formula:
#>   (b.m~x + (b.w1x)*(w1))*(b.y~m + (b.w2m)*(w2))
#> 
#> Computation:
#>   ((-0.66304) + (0.20389)*(6.17316))*((-0.15271) + (0.20376)*(4.04049))
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>  Path Conditional Effect Original Coefficient
#>   m~x              0.596               -0.663
#>   y~m              0.671               -0.153

Changing the Levels of the Moderators

The levels of the moderators, w1 and w2 in this example, can be controlled directly by users. For examples, percentiles or exact values of the moderators can be used. See vignette("mod_levels") on how to specify other levels of the moderators, and the arguments w_method, sd_from_mean, and percentiles of cond_indirect_effects().

Standardized Conditional Indirect Effects

To compute the standardized conditional indirect effects, we can standardize only the predictor (x), only the outcome (y), or both.

To standardize x, set standardized_x to TRUE. To standardize y, set standardized_y to TRUE. To standardize both, set both standardized_x and standardized_y to TRUE.

This is the result when both x and y are standardized:

out_cond_stdxy <- cond_indirect_effects(wlevels =c("w1", "w2"),
                                        x = "x",
                                        y = "y",
                                        m = "m",
                                        fit = fit,
                                        boot_ci = TRUE,
                                        boot_out = fit_boot,
                                        standardized_x = TRUE,
                                        standardized_y = TRUE)

Note that fit_boot is used so that there is no need to do bootstrapping again.

This is the output:

out_cond_stdxy
#> 
#> == Conditional indirect effects ==
#> 
#>  Path: x -> m -> y
#>  Conditional on moderator(s): w1, w2
#>  Moderator(s) represented by: w1, w2
#> 
#>      [w1]    [w2]  (w1)  (w2)   std  CI.lo CI.hi Sig   m~x   y~m   ind
#> 1 M+1.0SD M+1.0SD 6.173 4.040 0.401  0.154 0.655 Sig 0.596 0.671 0.399
#> 2 M+1.0SD M-1.0SD 6.173 2.055 0.159 -0.029 0.363     0.596 0.266 0.158
#> 3 M-1.0SD M+1.0SD 4.038 4.040 0.108 -0.145 0.370     0.160 0.671 0.107
#> 4 M-1.0SD M-1.0SD 4.038 2.055 0.043 -0.062 0.190     0.160 0.266 0.043
#> 
#>  - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#>    nonparametric bootstrapping with 500 samples.
#>  - std: The standardized conditional indirect effects. 
#>  - ind: The unstandardized conditional indirect effects.
#>  - 'm~x','y~m' is/are the path coefficient(s) along the path conditional
#>    on the moderator(s).

The standardized indirect effect when both w1 and w2 are one SD above mean is 0.401, with 95% bootstrap confidence interval [0.154, 0.655].

That is, when both w1 and w2 are one SD above their means, if x increases by one SD, it leads to an increase of 0.401 SD of y through m.

Index of Moderated Moderated Mediation

The index of moderated moderated mediation (Hayes, 2018) can be estimated, along with bootstrap confidence interval, using the function index_of_momome():

out_momome <- index_of_momome(x = "x",
                              y = "y",
                              m = "m",
                              w = "w1",
                              z = "w2",
                              fit = fit,
                              boot_ci = TRUE,
                              boot_out = fit_boot)

These are the major arguments:

x: The name of the predictor.
y: The name of the outcome variable.
m: The name of the mediator, or a vector of names if the path has more than one mediator (see this example).
w: The name of one of the moderator.
z: The name of the other moderator. The order of w and z does not matter.
fit: The output of lavaan::sem().
boot_ci: Set to TRUE to request bootstrap confidence intervals. Default is FALSE.
boot_out: The pregenerated bootstrap estimates generated by do_boot() or previous call to cond_indirect_effects() and indirect_effect().

This is the result:

out_momome
#> 
#> == Conditional indirect effects ==
#> 
#>  Path: x -> m -> y
#>  Conditional on moderator(s): w1, w2
#>  Moderator(s) represented by: w1, w2
#> 
#>   [w1] [w2] (w1) (w2)    ind  CI.lo CI.hi Sig    m~x    y~m
#> 1    1    1    1    1 -0.023 -0.276 0.312     -0.459  0.051
#> 2    1    0    1    0  0.070 -0.206 0.649     -0.459 -0.153
#> 3    0    1    0    1 -0.034 -0.364 0.383     -0.663  0.051
#> 4    0    0    0    0  0.101 -0.252 0.868     -0.663 -0.153
#> 
#> == Index of Moderated Moderated Mediation ==
#> 
#> Levels compared:
#> (Row 1 - Row 2) - (Row 3 - Row 4)
#> 
#>       x y Index  CI.lo CI.hi
#> Index x y 0.042 -0.003 0.116
#> 
#>  - [CI.lo, CI.hi]: 95% percentile confidence interval.

The index of moderated moderated mediation is 0.042, with 95% bootstrap confidence interval [-0.003, 0.116].

Note that this index is specifically for the change when w1 or w2 increases by one unit.

Index of Moderated Mediation

The manymome package also has a function to compute the index of moderated mediation (Hayes, 2015). Suppose we modify the model and remove one of the moderators:

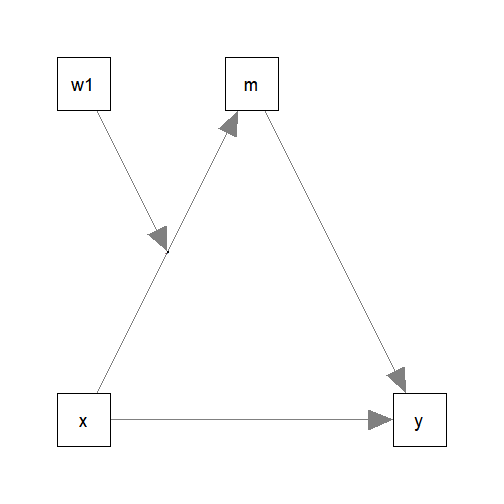
plot of chunk manymome_plot_mome1

This is the lavaan model:

library(lavaan)
dat$w1x <- dat$w1 * dat$x
mod2 <-
"
m ~ x + w1 + w1x + c1 + c2
y ~ m + x + c1 + c2
"
fit2 <- sem(model = mod2,
           data = dat,
           fixed.x = FALSE,
           estimator = "MLR")

These are the parameter estimates of the paths:

parameterEstimates(fit2)[parameterEstimates(fit2)$op == "~", ]
#>   lhs op rhs    est    se      z pvalue ci.lower ci.upper
#> 1   m  ~   x -0.663 0.533 -1.244  0.213   -1.707    0.381
#> 2   m  ~  w1 -2.290 1.010 -2.267  0.023   -4.269   -0.310
#> 3   m  ~ w1x  0.204 0.101  2.023  0.043    0.006    0.401
#> 4   m  ~  c1 -0.020 0.079 -0.251  0.801   -0.175    0.135
#> 5   m  ~  c2 -0.130 0.090 -1.444  0.149   -0.306    0.046
#> 6   y  ~   m  0.434 0.114  3.815  0.000    0.211    0.657
#> 7   y  ~   x  0.053 0.093  0.570  0.569   -0.130    0.237
#> 8   y  ~  c1 -0.108 0.080 -1.352  0.177   -0.265    0.049
#> 9   y  ~  c2 -0.077 0.085 -0.904  0.366   -0.243    0.090

We generate the bootstrap estimates first (R should be 2000 or even 5000 in real research):

fit2_boot <- do_boot(fit = fit2,
                    R = 500,
                    seed = 53253,
                    ncores = 1)

The function index_of_mome() can be used to compute the index of moderated mediation of w1 on the path x -> m -> y:

out_mome <- index_of_mome(x = "x",
                          y = "y",
                          m = "m",
                          w = "w1",
                          fit = fit2,
                          boot_ci = TRUE,
                          boot_out = fit2_boot)

The arguments are nearly identical to those of index_of_momome(), except that only w needs to be specified. This is the output:

out_mome
#> 
#> == Conditional indirect effects ==
#> 
#>  Path: x -> m -> y
#>  Conditional on moderator(s): w1
#>  Moderator(s) represented by: w1
#> 
#>   [w1] (w1)    ind  CI.lo CI.hi Sig    m~x   y~m
#> 1    1    1 -0.199 -0.762 0.230     -0.459 0.434
#> 2    0    0 -0.288 -0.998 0.222     -0.663 0.434
#> 
#> == Index of Moderated Mediation ==
#> 
#> Levels compared: Row 1 - Row 2
#> 
#>       x y Index  CI.lo CI.hi
#> Index x y 0.088 -0.006 0.223
#> 
#>  - [CI.lo, CI.hi]: 95% percentile confidence interval.

In this model, the index of moderated mediation is 0.088, with 95% bootstrap confidence interval [-0.006, 0.223]. The indirect effect of x on y through m does not significantly change when w1 increases by one unit.

Note that this index is specifically for the change when w1 increases by one unit. The index being not significant does not contradict with the significant moderation effect suggested by the product term.

Mediation Only

The package can also be used for a mediation model.

This is the sample data set that comes with the package:

library(manymome)
dat <- data_serial
print(head(dat), digits = 3)
#>       x   m1    m2     y        c1   c2
#> 1 12.12 20.6  9.33  9.00  0.109262 6.01
#> 2  9.81 18.2  9.47 11.56 -0.124014 6.42
#> 3 10.11 20.3 10.05  9.35  4.278608 5.34
#> 4 10.07 19.7 10.17 11.41  1.245356 5.59
#> 5 11.91 20.5 10.05 14.26 -0.000932 5.34
#> 6  9.13 16.5  8.93 10.01  1.802727 5.91

Suppose this is the model being fitted, with c1 and c2 the control variables.

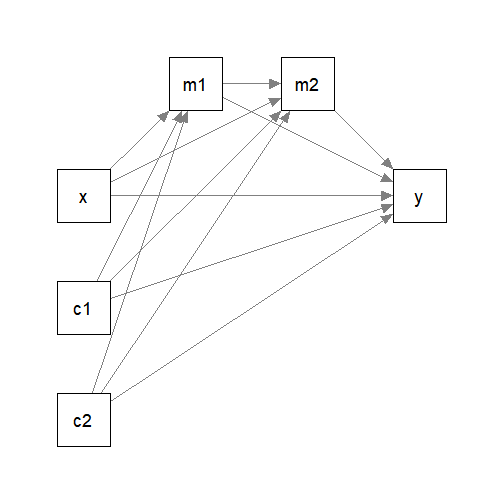
plot of chunk manymome_draw_med

Fitting the Model

Fitting this model in lavaan::sem() is very simple. With manymome, there is no need to label paths or define user parameters for the indirect effects.

mod_med <- "
m1 ~ x + c1 + c2
m2 ~ m1 + x + c1 + c2
y ~ m2 + m1 + x + c1 + c2
"
fit_med <- sem(model = mod_med,
               data = dat,
               fixed.x = TRUE)

These are the estimates of the paths:

parameterEstimates(fit_med)[parameterEstimates(fit_med)$op == "~", ]
#>    lhs op rhs    est    se      z pvalue ci.lower ci.upper
#> 1   m1  ~   x  0.822 0.092  8.907  0.000    0.641    1.003
#> 2   m1  ~  c1  0.171 0.089  1.930  0.054   -0.003    0.346
#> 3   m1  ~  c2 -0.189 0.091 -2.078  0.038   -0.367   -0.011
#> 4   m2  ~  m1  0.421 0.099  4.237  0.000    0.226    0.615
#> 5   m2  ~   x -0.116 0.123 -0.946  0.344   -0.357    0.125
#> 6   m2  ~  c1  0.278 0.090  3.088  0.002    0.101    0.454
#> 7   m2  ~  c2 -0.162 0.092 -1.756  0.079   -0.343    0.019
#> 8    y  ~  m2  0.521 0.221  2.361  0.018    0.088    0.953
#> 9    y  ~  m1 -0.435 0.238 -1.830  0.067   -0.902    0.031
#> 10   y  ~   x  0.493 0.272  1.811  0.070   -0.040    1.026
#> 11   y  ~  c1  0.099 0.208  0.476  0.634   -0.308    0.506
#> 12   y  ~  c2 -0.096 0.207 -0.465  0.642   -0.501    0.309

Estimate Indirect Effects

indirect_effect() can be used to estimate an indirect effect and form its bootstrapping confidence interval along a path in a model that starts with any numeric variable, ends with any numeric variable, through any numeric variable(s).

We illustrate another approach to generate bootstrap estimates: using indirect_effect() to do both bootstrapping and estimate the indirect effect.

For example, this is the call for the indirect effect from x to y through m1 and m2:

out_med <- indirect_effect(x = "x",
                           y = "y",
                           m = c("m1", "m2"),
                           fit = fit_med,
                           boot_ci = TRUE,
                           R = 500,
                           seed = 43143,
                           ncores = 1)

The main arguments are:

x: The name of the predictor. The start of the path.
y: The name of the outcome variable. The end of the path.
m: The name of the mediator, or the vector of names of the mediators if the path has more than one mediator, as in this example. The path moves from the first mediator to the last mediator. In this example, the correct order is c("m1", "m2").
fit: The output of lavaan::sem().
boot_ci: Set to TRUE to request bootstrapping confidence intervals. Default is FALSE.
R: The number of bootstrap samples. Only 500 bootstrap samples for illustration. Set R to 2000 or even 5000 in real research.
seed: The seed for the random number generator.
ncores: The number of processes in parallel processing. The default number is the number of detected physical cores minus 1. Can be omitted in real studies. Set to 1 here for illustration.

Like do_boot(), by default, parallel processing is used, and so the results are reproducible with the same seed only if the number of processes (cores) is the same.

This is the output:

out_med
#> 
#> == Indirect Effect  ==
#>                                        
#>  Path:               x -> m1 -> m2 -> y
#>  Indirect Effect:    0.180             
#>  95.0% Bootstrap CI: [0.034 to 0.396]  
#> 
#> Computation Formula:
#>   (b.m1~x)*(b.m2~m1)*(b.y~m2)
#> 
#> Computation:
#>   (0.82244)*(0.42078)*(0.52077)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>   Path Coefficient
#>   m1~x       0.822
#>  m2~m1       0.421
#>   y~m2       0.521

The indirect effect from x to y through m1 and m2 is 0.180, with a 95% confidence interval of [0.034, 0.396], significantly different from zero (p < .05).

Because bootstrap confidence interval is requested, the bootstrap estimates are stored in out_med. This output from indirect_effect() can also be used in the argument boot_out of other functions.

Standardized Indirect Effect

To compute the indirect effect with the predictor standardized, set standardized_x to TRUE. To compute the indirect effect with the outcome variable standardized, set standardized_y to TRUE. To compute the (completely) standardized indirect effect, set both standardized_x and standardized_y to TRUE.

This is the call to compute the (completely) standardized indirect effect:

out_med_stdxy <- indirect_effect(x = "x",
                                 y = "y",
                                 m = c("m1", "m2"),
                                 fit = fit_med,
                                 boot_ci = TRUE,
                                 boot_out = out_med,
                                 standardized_x = TRUE,
                                 standardized_y = TRUE)
out_med_stdxy
#> 
#> == Indirect Effect (Both 'x' and 'y' Standardized) ==
#>                                        
#>  Path:               x -> m1 -> m2 -> y
#>  Indirect Effect:    0.086             
#>  95.0% Bootstrap CI: [0.017 to 0.183]  
#> 
#> Computation Formula:
#>   (b.m1~x)*(b.m2~m1)*(b.y~m2)*sd_x/sd_y
#> 
#> Computation:
#>   (0.82244)*(0.42078)*(0.52077)*(0.95010)/(1.99960)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>   Path Coefficient
#>   m1~x       0.822
#>  m2~m1       0.421
#>   y~m2       0.521
#> 
#> NOTE:
#> - The effects of the component paths are from the model, not
#>   standardized.

The indirect effect from x to y through m1 and m2 is 0.086, with a 95% confidence interval of [0.017, 0.183], significantly different from zero (p < .05). One SD increase of x leads to 0.086 increase in SD of y through m1 and m2.

Estimating Indirect Effects For Any Paths

indirect_effect() can be used for the indirect effect in any path in a path model.

For example, to estimate and test the indirect effect from x through m2 to y, bypassing m1, simply set x to "x", y to "y", and m to "m2":

out_x_m2_y <- indirect_effect(x = "x",
                              y = "y",
                              m = "m2",
                              fit = fit_med,
                              boot_ci = TRUE,
                              boot_out = out_med)
out_x_m2_y
#> 
#> == Indirect Effect  ==
#>                                       
#>  Path:               x -> m2 -> y     
#>  Indirect Effect:    -0.060           
#>  95.0% Bootstrap CI: [-0.232 to 0.097]
#> 
#> Computation Formula:
#>   (b.m2~x)*(b.y~m2)
#> 
#> Computation:
#>   (-0.11610)*(0.52077)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>  Path Coefficient
#>  m2~x      -0.116
#>  y~m2       0.521

The indirect effect along this path is not significant.

Similarly, indirect effects from m1 through m2 to y or from x through m1 to y can also be tested by setting the three arguments accordingly. Although c1 and c2 are labelled as control variables, if appropriate, their indirect effects on y through m1 and/or m2 can also be computed and tested.

Total Indirect Effects and Total Effects

Addition (+) and subtraction (-) can be applied to the outputs of indirect_effect(). For example, the total indirect effect from x to y is the sum of these indirect effects:

x -> m1 -> m2 -> y
x -> m1 -> y
x -> m2 -> y

Two of them have been computed above (out_med and out_x_m2_y). We compute the indirect effect in x -> m1 -> y

out_x_m1_y <- indirect_effect(x = "x",
                              y = "y",
                              m = "m1",
                              fit = fit_med,
                              boot_ci = TRUE,
                              boot_out = out_med)
out_x_m1_y
#> 
#> == Indirect Effect  ==
#>                                        
#>  Path:               x -> m1 -> y      
#>  Indirect Effect:    -0.358            
#>  95.0% Bootstrap CI: [-0.747 to -0.017]
#> 
#> Computation Formula:
#>   (b.m1~x)*(b.y~m1)
#> 
#> Computation:
#>   (0.82244)*(-0.43534)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>  Path Coefficient
#>  m1~x       0.822
#>  y~m1      -0.435

We can then “add” the indirect effects to get the total indirect effect:

total_ind <- out_med + out_x_m1_y + out_x_m2_y
total_ind
#> 
#> == Indirect Effect  ==
#>                                         
#>  Path:                x -> m1 -> m2 -> y
#>  Path:                x -> m1 -> y      
#>  Path:                x -> m2 -> y      
#>  Function of Effects: -0.238            
#>  95.0% Bootstrap CI:  [-0.596 to 0.092] 
#> 
#> Computation of the Function of Effects:
#>  ((x->m1->m2->y)
#> +(x->m1->y))
#> +(x->m2->y) 
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.

The total indirect effect is -0.238, not significant. This is an example of inconsistent mediation: some of the indirect Effects are positive and some are negative:

coef(out_med)
#>       y~x 
#> 0.1802238
coef(out_x_m1_y)
#>        y~x 
#> -0.3580391
coef(out_x_m2_y)
#>       y~x 
#> -0.060461

Similarly, the total effect of x on y can be computed by adding all the effects, direct or indirect. The direct effect can be computed with m not set:

out_x_direct <- indirect_effect(x = "x",
                                y = "y",
                                fit = fit_med,
                                boot_ci = TRUE,
                                boot_out = out_med)
out_x_direct
#> 
#> ==  Effect  ==
#>                                       
#>  Path:               x -> y           
#>  Effect:             0.493            
#>  95.0% Bootstrap CI: [-0.041 to 1.045]
#> 
#> Computation Formula:
#>   (b.y~x)
#> 
#> Computation:
#>   (0.49285)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.

This is the total effect:

total_effect <- out_med + out_x_m1_y + out_x_m2_y + out_x_direct
total_effect
#> 
#> == Indirect Effect  ==
#>                                         
#>  Path:                x -> m1 -> m2 -> y
#>  Path:                x -> m1 -> y      
#>  Path:                x -> m2 -> y      
#>  Path:                x -> y            
#>  Function of Effects: 0.255             
#>  95.0% Bootstrap CI:  [-0.200 to 0.731] 
#> 
#> Computation of the Function of Effects:
#>  (((x->m1->m2->y)
#> +(x->m1->y))
#> +(x->m2->y))
#> +(x->y) 
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.

The total effect is 0.255, not significant. This illustrates that total effect can be misleading when the component paths are of different signs.

See help(math_indirect) for more information of addition and subtraction for the output of indirect_effect().

Summary

Advantages

The model fitting stage is easier. No need to label any parameters or define any effects. Users can also use other methods for confidence interval and use bootstrapping only for indirect effects and conditional indirect effects.
Missing data can be be handled by missing = "fiml" in calling lavaan::sem(). Because bootstrapping estimates are used in Stage 2, indirect effects and conditional indirect effects can also be computed with bootstrap confidence intervals, just like defining them in lavaan, in the presence of missing data.
Missing data handled by multiple imputation is also supported since version 0.1.9.8. Models fitted by semTools::sem.mi() or semTools::runMI() to multiple imputation datasets can be used just like the output of lavaan::sem(). Monte Carlo confidence intervals cna be formed for effects computed for these models (see vignette("do_mc_lavaan_mi")).
Bootstrapping only needs to be done once. The bootstrap estimates can be reused in computing indirect effects and conditional indirect effects. This is particularly useful when the sample size is large and there is missing data.
Users can explore any path for any levels of the moderators without respecifying and refitting the model.
Flexibility makes it difficult to test all possible scenarios. Therefore, the print methods will also print the details of the computation (e.g., how an indirect effect is computed) so that users can (a) understand how each effect is computed, and (b) verify the computation if necessary.

See this section for other advantages.

Limitations

The package manymome supports “many” models … but certainly not all. There are models that it does not yet support. For example, it does not support a path that starts with a nominal categorical variable (except for a dichotomous variable). Other tools need to be used for these cases. See this section for other limitations.

Other Uses and Scenarios

There are other options available in manymome. For example, it can be used for categorical moderators and models fitted by multiple regression. Please refer to the help page and examples of the functions, or other articles. More articles will be added in the future for other scenarios.

Monte Carlo Confidence Intervals

Monte Carlo confidence intervals can also be formed using the functions illustrated above. First use do_mc() instead of do_boot() to generate simulated sample estimates. When calling other main functions, use mc_ci = TRUE and set mc_out to the output of do_mc(). Please refer to vignette("do_mc") for an illustration, and vignette("do_mc_lavaan_mi") on how to form Monte Carlo confidence intervals for models fitted to multiple imputation datasets.

References

Cheung, M. W.-L. (2009). Comparison of methods for constructing confidence intervals of standardized indirect effects. Behavior Research Methods, 41(2), 425-438. https://doi.org/10.3758/BRM.41.2.425

Cheung, S. F., & Cheung, S.-H. (2023). manymome: An R package for computing the indirect effects, conditional effects, and conditional indirect effects, standardized or unstandardized, and their bootstrap confidence intervals, in many (though not all) models. Behavior Research Methods. https://doi.org/10.3758/s13428-023-02224-z

Falk, C. F., & Biesanz, J. C. (2015). Inference and interval estimation methods for indirect effects with latent variable models. Structural Equation Modeling: A Multidisciplinary Journal, 22(1), 24–38. https://doi.org/10.1080/10705511.2014.935266

Friedrich, R. J. (1982). In defense of multiplicative terms in multiple regression equations. American Journal of Political Science, 26(4), 797-833. https://doi.org/10.2307/2110973

Hayes, A. F. (2015). An index and test of linear moderated mediation. Multivariate Behavioral Research, 50(1), 1-22. https://doi.org/10.1080/00273171.2014.962683

Hayes, A. F. (2018). Partial, conditional, and moderated moderated mediation: Quantification, inference, and interpretation. Communication Monographs, 85(1), 4-40. https://doi.org/10.1080/03637751.2017.1352100

Hayes, A. F. (2022). Introduction to mediation, moderation, and conditional process analysis: A regression-based approach (Third Edition). The Guilford Press.

Kwan, J. L. Y., & Chan, W. (2018). Variable system: An alternative approach for the analysis of mediated moderation. Psychological Methods, 23(2), 262-277. https://doi.org/10.1037/met0000160

Miles, J. N. V., Kulesza, M., Ewing, B., Shih, R. A., Tucker, J. S., & D’Amico, E. J. (2015). Moderated mediation analysis: An illustration using the association of gender with delinquency and mental health. Journal of Criminal Psychology, 5(2), 99-123. https://doi.org/10.1108/JCP-02-2015-0010

Tofighi, D., & Kelley, K. (2020). Indirect effects in sequential mediation models: Evaluating methods for hypothesis testing and confidence interval formation. Multivariate Behavioral Research, 55(2), 188–210. https://doi.org/10.1080/00273171.2019.1618545

Shu Fai Cheung & Sing-Hang Cheung

2024-12-04

Introduction

Workflow

What Will Be Covered In This Get-Started Article

Moderated Mediation by SEM using `lavaan`

Fitting the Model

Conditional Indirect Effects

Do Bootstrapping (Once)

Estimate Conditional Indirect Effects

Examine the Effect at a Particular Set of Levels of the Moderators

Changing the Levels of the Moderators

Standardized Conditional Indirect Effects

Index of Moderated Moderated Mediation

Index of Moderated Mediation

Mediation Only

Fitting the Model

Estimate Indirect Effects

Standardized Indirect Effect

Estimating Indirect Effects For Any Paths

Total Indirect Effects and Total Effects

Summary

Advantages

Limitations

Other Uses and Scenarios

Monte Carlo Confidence Intervals

References

manymome

Shu Fai Cheung & Sing-Hang Cheung

2024-12-04

Introduction

Workflow

What Will Be Covered In This Get-Started Article

Moderated Mediation by SEM using lavaan

Fitting the Model

Conditional Indirect Effects

Do Bootstrapping (Once)

Estimate Conditional Indirect Effects

Examine the Effect at a Particular Set of Levels of the Moderators

Changing the Levels of the Moderators

Standardized Conditional Indirect Effects

Index of Moderated Moderated Mediation

Index of Moderated Mediation

Mediation Only

Fitting the Model

Estimate Indirect Effects

Standardized Indirect Effect

Estimating Indirect Effects For Any Paths

Total Indirect Effects and Total Effects

Summary

Advantages

Limitations

Other Uses and Scenarios

Monte Carlo Confidence Intervals

References

Moderated Mediation by SEM using `lavaan`