All-In-One Functions for Common Mediation Models
Shu Fai Cheung & Sing-Hang Cheung
2025-08-10
Source:vignettes/articles/q_mediation.Rmd
q_mediation.RmdIntroduction
This article is a brief illustration of how to use the new all-in-one “quick” functions from manymome (Cheung & Cheung, 2024) to fit the regression models and compute and test indirect effects in one step.
The following sections on the three models, simple mediation model, serial mediation model, and parallel mediation model has sections duplicated, to make each section self-contained.
Simple Mediation Model
This is the sample data set that comes with the package for this example:
library(manymome)
dat <- data_med
print(head(dat), digits = 3)
#> x m y c1 c2
#> 1 9.93 17.9 20.7 1.43 6.10
#> 2 8.33 17.9 22.9 2.94 3.83
#> 3 10.33 17.8 22.1 3.01 5.77
#> 4 11.20 20.0 25.1 3.12 4.65
#> 5 11.89 22.1 28.5 4.44 3.96
#> 6 8.20 17.0 20.7 2.50 3.76Suppose we would like to fit a simple mediation model with only one
mediator, with c1 and c2 as the control
variables.
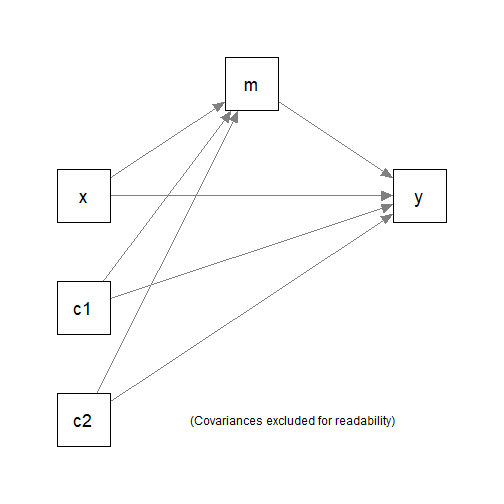
We would to fit the two regression models
m ~ x + c1 + c2y ~ m + x + c1 + c2
and the compute and test the indirect effect along the path
x -> m -> y using nonparametric bootstrapping.
Analysis
We can do that in one single step using
q_simple_mediation():
out_simple <- q_simple_mediation(x = "x",
y = "y",
m = "m",
cov = c("c2", "c1"),
data = data_med,
R = 5000,
seed = 1234)These are the arguments:
x: The name of the predictor (“x” variable).y: The name of the outcome (“y” variable).m: The name of the mediator (“m” variable).cov: The name(s) of the control variable(s) (covariate(s)). By default, they predict both the mediator and the outcome.data: The data frame for the model.R: The number of bootstrap samples. Should be at least 5000 but can be larger for stable results.seed: The seed for the random number generator. Should always be set to an integer to make the results reproducible.
The computation may take some time to run but should be at most one or two minutes for contemporary computers.
Results
We can then just print the output:
out_simple
#>
#> =============== Simple Mediation Model ===============
#>
#> Call:
#>
#> q_simple_mediation(x = "x", y = "y", m = "m", cov = c("c2", "c1"),
#> data = data_med, R = 5000, seed = 1234)
#>
#> ===================================================
#> | Basic Information |
#> ===================================================
#>
#> Predictor(x): x
#> Outcome(y): y
#> Mediator(s)(m): m
#> Model: Simple Mediation Model
#>
#> The regression models fitted:
#>
#> m ~ x + c2 + c1
#> y ~ m + x + c2 + c1
#>
#> The number of cases included: 100
#>
#> ===================================================
#> | Regression Results |
#> ===================================================
#>
#>
#> Model:
#> m ~ x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 9.6894 7.8636 11.5152 0.0000 0.9198 10.5344 0.0000 ***
#> x 0.9347 0.7742 1.0951 0.7536 0.0808 11.5632 0.0000 ***
#> c2 -0.1684 -0.3730 0.0361 -0.1070 0.1030 -1.6343 0.1055
#> c1 0.1978 0.0454 0.3502 0.1676 0.0768 2.5759 0.0115 *
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: m, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.598. Adjusted R-square = 0.586. F(3, 96) = 47.622, p < .001
#>
#> Model:
#> y ~ m + x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 4.4152 -2.1393 10.9698 0.0000 3.3016 1.3373 0.1843
#> m 0.7847 0.2894 1.2800 0.4079 0.2495 3.1450 0.0022 **
#> x 0.5077 -0.0992 1.1145 0.2128 0.3057 1.6608 0.1000
#> c2 -0.1544 -0.6614 0.3526 -0.0510 0.2554 -0.6045 0.5470
#> c1 0.1405 -0.2448 0.5258 0.0619 0.1941 0.7239 0.4709
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: y, m, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.358. Adjusted R-square = 0.331. F(4, 95) = 13.220, p < .001
#>
#> ===================================================
#> | Indirect Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) ==
#>
#> ind CI.lo CI.hi Sig pvalue SE
#> x -> m -> y 0.7334 0.3051 1.1965 Sig 0.0012 0.2273
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - The 'ind' column shows the indirect effect(s).
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (x-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m -> y 0.7739 0.3223 1.2653 Sig 0.0012 0.2429
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized indirect effect(s).
#> - x-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m -> y 0.2914 0.1262 0.4686 Sig 0.0012 0.0864
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized indirect effect(s).
#> - y-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (Both x-variable(s) and y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m -> y 0.3074 0.1313 0.4876 Sig 0.0012 0.0912
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The standardized indirect effect(s).
#>
#> ===================================================
#> | Direct Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) ==
#>
#> ind CI.lo CI.hi Sig pvalue SE
#> x -> y 0.5077 -0.1436 1.1418 0.1292 0.3297
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - The 'ind' column shows the effect(s).
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (x-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.5357 -0.1571 1.2035 0.1292 0.3426
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized effect(s).
#> - x-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.2017 -0.0571 0.4590 0.1292 0.1319
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized effect(s).
#> - y-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (Both x-variable(s) and y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.2128 -0.0612 0.4754 0.1292 0.1365
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The standardized effect(s).
#>
#> ===================================================
#> | Notes |
#> ===================================================
#>
#> - For reference, the bootstrap confidence interval (and bootstrap
#> p-value, if requested) of the (unstandardized) direct effect is also
#> reported. The bootstrap p-value and the OLS t-statistc p-value can be
#> different.
#> - For the direct effects with either 'x'-variable or 'y'-variable, or
#> both, standardized, it is recommended to use the bootstrap confidence
#> intervals, which take into account the sampling error of the sample
#> standard deviations.
#> - The asymmetric bootstrap value for an effect is the same whether x
#> and/or y is/are standardized.These are the main sections of the default results:
Basic Information
The variables, the models, and the number of cases. Listwise deletion is used and only cases without missing data on all variables in the models are used.
Regression Results
This part is simply the usual outputs of regression analysis
conducted by lm().
Indirect Effect Results
By default, this section prints the estimated indirect effect, confidence interval, and asymmetric bootstrap p-value.
Four sections will be printed:
The original indirect effect.
The indirect effect with the predictor (“x”) standardized.
The indirect effect with the outcome (“y”) standardized.
The indirect effect with both the predictor (“x”) and the outcome (“y”) standardized, also called the completely standardized indirect effect or simply the standardized indirect effect.
These four versions of the results are printed by default such that users can select and interpret sections as they see fit.
Direct Effect Results
By default, this section prints the estimated direct effect (from the predictor “x” to the outcome “y”, not mediated), confidence interval, and asymmetric bootstrap p-value.
The OLS t-test of the direct effect is already available in section Regression Results. The bootstrap results are printed in case users prefer using the same confidence interval method for all the effects.
Serial Mediation Model
(Some sections are copied from the previous section to make this section self-contained and readers do not need to refer to the sections on other models.)
This is the sample data set that comes with the package for this example:
library(manymome)
dat <- data_serial
print(head(dat), digits = 3)
#> x m1 m2 y c1 c2
#> 1 12.12 20.6 9.33 9.00 0.109262 6.01
#> 2 9.81 18.2 9.47 11.56 -0.124014 6.42
#> 3 10.11 20.3 10.05 9.35 4.278608 5.34
#> 4 10.07 19.7 10.17 11.41 1.245356 5.59
#> 5 11.91 20.5 10.05 14.26 -0.000932 5.34
#> 6 9.13 16.5 8.93 10.01 1.802727 5.91Suppose we would like to fit a serial mediation model with two
mediators, with c1 and c2 as the control
variables.
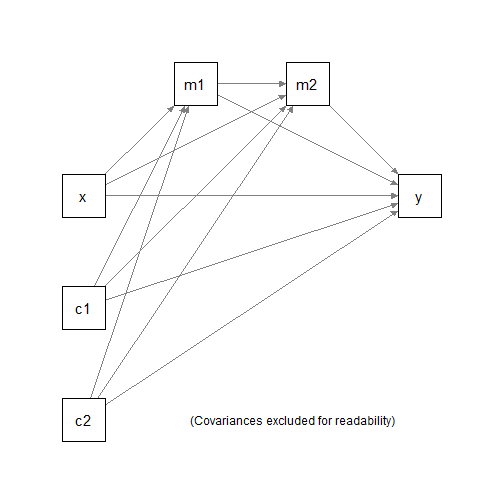
We would to fit three regression models:
m1 ~ x + c1 + c2m2 ~ m1 + x + c1 + c2y ~ m1 + m2 + x + c1 + c2
and the compute and test the following indirect effects:
x -> m1 -> m2 -> yx -> m1 -> yx -> m2 -> y
using nonparametric bootstrapping.
Analysis
We can do that in one single step using
q_serial_mediation():
out_serial <- q_serial_mediation(x = "x",
y = "y",
m = c("m1", "m2"),
cov = c("c2", "c1"),
data = data_serial,
R = 5000,
seed = 1234)These are the arguments:
x: The name of the predictor (“x” variable).y: The name of the outcome (“y” variable).m: A vector of the names of the mediators (“m” variables). The order of the names represents the order of the mediators, from the first name to the last name. Therefore, if the path isx -> m1 -> m2 -> y, set this toc("m1", "m2").cov: The name(s) of the control variable(s) (covariate(s)). By default, they predict all the mediators and the outcome.data: The data frame for the model.R: The number of bootstrap samples. Should be at least 5000 but can be larger for stable results.seed: The seed for the random number generator. Should always be set to an integer to make the results reproducible.
The computation will take longer to run for a serial mediation model,
and can be a few minutes if R is large.
Results
We can then just print the output:
out_serial
#>
#> =============== Serial Mediation Model ===============
#>
#> Call:
#>
#> q_serial_mediation(x = "x", y = "y", m = c("m1", "m2"), cov = c("c2",
#> "c1"), data = data_serial, R = 5000, seed = 1234)
#>
#> ===================================================
#> | Basic Information |
#> ===================================================
#>
#> Predictor(x): x
#> Outcome(y): y
#> Mediator(s)(m): m1, m2
#> Model: Serial Mediation Model
#>
#> The regression models fitted:
#>
#> m1 ~ x + c2 + c1
#> m2 ~ x + m1 + c2 + c1
#> y ~ m1 + m2 + x + c2 + c1
#>
#> The number of cases included: 100
#>
#> ===================================================
#> | Regression Results |
#> ===================================================
#>
#>
#> Model:
#> m1 ~ x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 10.8157 8.5453 13.0861 -0.0000 1.1438 9.4560 0.0000 ***
#> x 0.8224 0.6354 1.0095 0.6493 0.0942 8.7274 0.0000 ***
#> c2 -0.1889 -0.3730 -0.0047 -0.1534 0.0928 -2.0355 0.0446 *
#> c1 0.1715 -0.0086 0.3515 0.1423 0.0907 1.8906 0.0617 .
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: m1, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.477. Adjusted R-square = 0.461. F(3, 96) = 29.235, p < .001
#>
#> Model:
#> m2 ~ x + m1 + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 3.5194 0.3692 6.6696 -0.0000 1.5868 2.2179 0.0289 *
#> x -0.1161 -0.3662 0.1340 -0.1036 0.1260 -0.9216 0.3591
#> m1 0.4208 0.2185 0.6230 0.4758 0.1019 4.1300 0.0001 ***
#> c2 -0.1619 -0.3497 0.0259 -0.1487 0.0946 -1.7120 0.0902 .
#> c1 0.2775 0.0945 0.4606 0.2603 0.0922 3.0096 0.0033 **
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: m2, x, m1, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.341. Adjusted R-square = 0.313. F(4, 95) = 12.290, p < .001
#>
#> Model:
#> y ~ m1 + m2 + x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 9.4679 2.3021 16.6336 0.0000 3.6090 2.6234 0.0102 *
#> m1 -0.4353 -0.9226 0.0519 -0.2620 0.2454 -1.7740 0.0793 .
#> m2 0.5208 0.0690 0.9725 0.2772 0.2275 2.2888 0.0243 *
#> x 0.4929 -0.0643 1.0500 0.2342 0.2806 1.7562 0.0823 .
#> c2 -0.0960 -0.5190 0.3269 -0.0469 0.2130 -0.4509 0.6531
#> c1 0.0988 -0.3261 0.5238 0.0493 0.2140 0.4618 0.6453
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: y, m1, m2, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.091. Adjusted R-square = 0.043. F(5, 94) = 1.893, p = 0.103
#>
#> ===================================================
#> | Indirect Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) ==
#>
#> ind CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> m2 -> y 0.1802 0.0260 0.3838 Sig 0.0172 0.0922
#> x -> m1 -> y -0.3580 -0.7063 -0.0010 Sig 0.0488 0.1768
#> x -> m2 -> y -0.0605 -0.2527 0.1019 0.4608 0.0875
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - The 'ind' column shows the indirect effect(s).
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (x-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> m2 -> y 0.1721 0.0236 0.3697 Sig 0.0172 0.0889
#> x -> m1 -> y -0.3419 -0.6865 -0.0010 Sig 0.0488 0.1714
#> x -> m2 -> y -0.0577 -0.2434 0.0939 0.4608 0.0835
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized indirect effect(s).
#> - x-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> m2 -> y 0.0897 0.0134 0.1874 Sig 0.0172 0.0448
#> x -> m1 -> y -0.1782 -0.3446 -0.0005 Sig 0.0488 0.0861
#> x -> m2 -> y -0.0301 -0.1284 0.0493 0.4608 0.0435
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized indirect effect(s).
#> - y-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (Both x-variable(s) and y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> m2 -> y 0.0856 0.0124 0.1805 Sig 0.0172 0.0431
#> x -> m1 -> y -0.1701 -0.3286 -0.0005 Sig 0.0488 0.0832
#> x -> m2 -> y -0.0287 -0.1221 0.0453 0.4608 0.0414
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The standardized indirect effect(s).
#>
#> ===================================================
#> | Total Indirect Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect ==
#>
#> Path: x -> m1 -> m2 -> y
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: -0.2383
#> 95.0% Bootstrap CI: [-0.5836 to 0.0956]
#> Bootstrap p-value: 0.1592
#> Bootstrap SE: 0.1679
#>
#> Computation of the Function of Effects:
#> ((x->m1->m2->y)
#> +(x->m1->y))
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect ('x' Standardized) ==
#>
#> Path: x -> m1 -> m2 -> y
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: -0.2275
#> 95.0% Bootstrap CI: [-0.5603 to 0.0890]
#> Bootstrap p-value: 0.1592
#> Bootstrap SE: 0.1619
#>
#> Computation of the Function of Effects:
#> ((x->m1->m2->y)
#> +(x->m1->y))
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect ('y' Standardized) ==
#>
#> Path: x -> m1 -> m2 -> y
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: -0.1186
#> 95.0% Bootstrap CI: [-0.2867 to 0.0485]
#> Bootstrap p-value: 0.1592
#> Bootstrap SE: 0.0832
#>
#> Computation of the Function of Effects:
#> ((x->m1->m2->y)
#> +(x->m1->y))
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect (Both 'x' and 'y' Standardized) ==
#>
#> Path: x -> m1 -> m2 -> y
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: -0.1132
#> 95.0% Bootstrap CI: [-0.2764 to 0.0455]
#> Bootstrap p-value: 0.1592
#> Bootstrap SE: 0.0800
#>
#> Computation of the Function of Effects:
#> ((x->m1->m2->y)
#> +(x->m1->y))
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ===================================================
#> | Direct Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) ==
#>
#> ind CI.lo CI.hi Sig pvalue SE
#> x -> y 0.4929 -0.0698 1.0292 0.0884 0.2817
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - The 'ind' column shows the effect(s).
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (x-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.4706 -0.0610 0.9876 0.0884 0.2698
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized effect(s).
#> - x-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.2452 -0.0364 0.5009 0.0884 0.1373
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized effect(s).
#> - y-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (Both x-variable(s) and y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.2342 -0.0318 0.4772 0.0884 0.1310
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The standardized effect(s).
#>
#> ===================================================
#> | Notes |
#> ===================================================
#>
#> - For reference, the bootstrap confidence interval (and bootstrap
#> p-value, if requested) of the (unstandardized) direct effect is also
#> reported. The bootstrap p-value and the OLS t-statistc p-value can be
#> different.
#> - For the direct effects with either 'x'-variable or 'y'-variable, or
#> both, standardized, it is recommended to use the bootstrap confidence
#> intervals, which take into account the sampling error of the sample
#> standard deviations.
#> - The asymmetric bootstrap value for an effect is the same whether x
#> and/or y is/are standardized.These are the main sections of the default results:
Basic Information
The variables, the models, and the number of cases. Listwise deletion is used and only cases without missing data on all variables in the models are used.
Regression Results
This part is simply the usual outputs of regression analysis
conducted by lm().
Indirect Effect Results
By default, this section prints the estimated indirect effects, confidence intervals, and asymmetric bootstrap p-values.
Four sections will be printed:
The original indirect effects.
The indirect effects with the predictor (“x”) standardized.
The indirect effects with the outcome (“y”) standardized.
The indirect effects with both the predictor (“x”) and the outcome (“y”) standardized, also called the completely standardized indirect effects or simply the standardized indirect effects.
These four versions of the results are printed by default such that users can select and interpret sections as they see fit.
Total Indirect Effect Results
By default, this section prints the estimated total indirect effects, confidence intervals, and asymmetric bootstrap p-values.
The total indirect effect in a serial mediation model is the sum of all indirect effects from the predictor (“x”) to the outcome (“y”).
Four sections will be printed:
The original total indirect effect.
The total indirect effects with the predictor (“x”) standardized.
The total indirect effects with the outcome (“y”) standardized.
The total indirect effects with both the predictor (“x”) and the outcome (“y”) standardized, also called the completely standardized total indirect effects or simply the standardized total indirect effects.
These four versions of the results are printed by default such that users can select and interpret sections as they see fit.
Direct Effect Results
By default, this section prints the estimated direct effect (from the predictor “x” to the outcome “y”, not mediated), confidence interval, and asymmetric bootstrap p-value.
The OLS t-test of the direct effect is already available in section Regression Results. The bootstrap results are printed in case users prefer using the same confidence interval method for all the effects.
Parallel Mediation Model
(Some sections are copied from the previous sections to make this section self-contained and readers do not need to refer to the sections on other models.)
This is the sample data set that comes with the package for this example:
library(manymome)
dat <- data_parallel
print(head(dat), digits = 3)
#> x m1 m2 y c1 c2
#> 1 9.65 20.8 8.98 16.9 2.39 4.01
#> 2 9.01 18.3 6.52 16.0 2.59 5.98
#> 3 9.34 18.0 6.27 20.1 2.67 4.17
#> 4 9.27 16.6 5.45 12.1 2.02 3.82
#> 5 9.85 18.3 6.85 15.6 3.80 4.38
#> 6 9.15 18.2 7.17 15.4 3.69 5.28Suppose we would like to fit a parallel mediation model with two
mediators, with c1 and c2 as the control
variables.
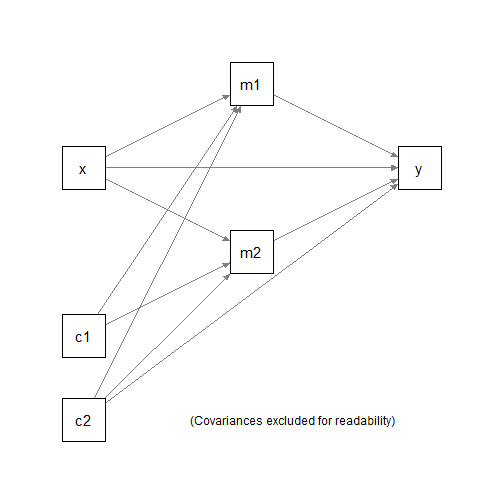
We would to fit three regression models:
m1 ~ x + c1 + c2m2 ~ x + c1 + c2y ~ m1 + m2 + x + c1 + c2
and the compute and test the following indirect effects:
x -> m1 -> yx -> m2 -> y
using nonparametric bootstrapping.
Analysis
We can do that in one single step using
q_parallel_mediation():
out_parallel <- q_parallel_mediation(x = "x",
y = "y",
m = c("m1", "m2"),
cov = c("c2", "c1"),
data = data_parallel,
R = 5000,
seed = 1234)These are the arguments:
x: The name of the predictor (“x” variable).y: The name of the outcome (“y” variable).m: A vector of the names of the mediators (“m” variables). For a parallel mediation model, the order of the mediators does not matter.cov: The name(s) of the control variable(s) (covariate(s)). By default, they predict all the mediators and the outcome.data: The data frame for the model.R: The number of bootstrap samples. Should be at least 5000 but can be larger for stable results.seed: The seed for the random number generator. Should always be set to an integer to make the results reproducible.
The computation will take longer to run for a parallel mediation
model, and can be a few minutes if R is large.
Results
We can then just print the output:
out_parallel
#>
#> =============== Parallel Mediation Model ===============
#>
#> Call:
#>
#> q_parallel_mediation(x = "x", y = "y", m = c("m1", "m2"), cov = c("c2",
#> "c1"), data = data_parallel, R = 5000, seed = 1234)
#>
#> ===================================================
#> | Basic Information |
#> ===================================================
#>
#> Predictor(x): x
#> Outcome(y): y
#> Mediator(s)(m): m1, m2
#> Model: Parallel Mediation Model
#>
#> The regression models fitted:
#>
#> m1 ~ x + c2 + c1
#> m2 ~ x + c2 + c1
#> y ~ m1 + m2 + x + c2 + c1
#>
#> The number of cases included: 100
#>
#> ===================================================
#> | Regression Results |
#> ===================================================
#>
#>
#> Model:
#> m1 ~ x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 9.3926 6.6132 12.1720 -0.0000 1.4002 6.7081 0.0000 ***
#> x 0.8769 0.6498 1.1040 0.6049 0.1144 7.6647 0.0000 ***
#> c2 -0.0929 -0.3362 0.1503 -0.0595 0.1225 -0.7584 0.4501
#> c1 0.2519 0.0309 0.4728 0.1742 0.1113 2.2630 0.0259 *
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: m1, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.439. Adjusted R-square = 0.422. F(3, 96) = 25.082, p < .001
#>
#> Model:
#> m2 ~ x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 4.3796 1.7071 7.0520 0.0000 1.3463 3.2530 0.0016 **
#> x 0.2968 0.0784 0.5151 0.2516 0.1100 2.6977 0.0082 **
#> c2 -0.3125 -0.5464 -0.0786 -0.2457 0.1178 -2.6517 0.0094 **
#> c1 0.2746 0.0621 0.4870 0.2334 0.1070 2.5655 0.0118 *
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: m2, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.217. Adjusted R-square = 0.193. F(3, 96) = 8.875, p < .001
#>
#> Model:
#> y ~ m1 + m2 + x + c2 + c1
#>
#> Estimate CI.lo CI.hi betaS Std. Error t value Pr(>|t|) Sig
#> (Intercept) 2.6562 -3.6518 8.9641 0.0000 3.1770 0.8361 0.4052
#> m1 0.4864 0.1071 0.8658 0.3016 0.1911 2.5459 0.0125 *
#> m2 0.4713 0.0767 0.8658 0.2378 0.1987 2.3718 0.0197 *
#> x 0.2911 -0.2438 0.8260 0.1245 0.2694 1.0807 0.2826
#> c2 -0.0321 -0.4970 0.4327 -0.0127 0.2341 -0.1372 0.8912
#> c1 -0.0526 -0.4806 0.3755 -0.0225 0.2156 -0.2438 0.8079
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> - BetaS are standardized coefficients with (a) only numeric variables
#> standardized and (b) product terms formed after standardization.
#> Variable(s) standardized is/are: y, m1, m2, x, c2, c1
#> - CI.lo and CI.hi are the 95.0% confidence levels of 'Estimate'
#> computed from the t values and standard errors.
#> R-square = 0.283. Adjusted R-square = 0.245. F(5, 94) = 7.420, p < .001
#>
#> ===================================================
#> | Indirect Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) ==
#>
#> ind CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> y 0.4266 0.1106 0.8068 Sig 0.0112 0.1778
#> x -> m2 -> y 0.1399 0.0066 0.3488 Sig 0.0332 0.0907
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - The 'ind' column shows the indirect effect(s).
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (x-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> y 0.4279 0.1066 0.8273 Sig 0.0112 0.1823
#> x -> m2 -> y 0.1403 0.0060 0.3500 Sig 0.0332 0.0914
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized indirect effect(s).
#> - x-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> y 0.1819 0.0501 0.3390 Sig 0.0112 0.0726
#> x -> m2 -> y 0.0596 0.0030 0.1427 Sig 0.0332 0.0368
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized indirect effect(s).
#> - y-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect(s) (Both x-variable(s) and y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> m1 -> y 0.1825 0.0479 0.3389 Sig 0.0112 0.0746
#> x -> m2 -> y 0.0598 0.0028 0.1436 Sig 0.0332 0.0371
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The standardized indirect effect(s).
#>
#> ===================================================
#> | Total Indirect Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect ==
#>
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: 0.5664
#> 95.0% Bootstrap CI: [0.2215 to 1.0202]
#> Bootstrap p-value: 0.0012
#> Bootstrap SE: 0.1989
#>
#> Computation of the Function of Effects:
#> (x->m1->y)
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect ('x' Standardized) ==
#>
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: 0.5682
#> 95.0% Bootstrap CI: [0.2159 to 1.0249]
#> Bootstrap p-value: 0.0012
#> Bootstrap SE: 0.2062
#>
#> Computation of the Function of Effects:
#> (x->m1->y)
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect ('y' Standardized) ==
#>
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: 0.2415
#> 95.0% Bootstrap CI: [0.1014 to 0.4101]
#> Bootstrap p-value: 0.0012
#> Bootstrap SE: 0.0771
#>
#> Computation of the Function of Effects:
#> (x->m1->y)
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ----------------------------------------------------------------
#>
#> == Indirect Effect (Both 'x' and 'y' Standardized) ==
#>
#> Path: x -> m1 -> y
#> Path: x -> m2 -> y
#> Function of Effects: 0.2423
#> 95.0% Bootstrap CI: [0.0975 to 0.4172]
#> Bootstrap p-value: 0.0012
#> Bootstrap SE: 0.0805
#>
#> Computation of the Function of Effects:
#> (x->m1->y)
#> +(x->m2->y)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 5000 bootstrap samples.
#> Standard error (SE) based on nonparametric bootstrapping with 5000
#> bootstrap samples.
#>
#>
#> ===================================================
#> | Direct Effect Results |
#> ===================================================
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) ==
#>
#> ind CI.lo CI.hi Sig pvalue SE
#> x -> y 0.2911 -0.1886 0.7405 0.2264 0.2346
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - The 'ind' column shows the effect(s).
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (x-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.2920 -0.1918 0.7122 0.2264 0.2309
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized effect(s).
#> - x-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.1241 -0.0810 0.3190 0.2264 0.1017
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The partially standardized effect(s).
#> - y-variable(s) standardized.
#>
#> ----------------------------------------------------------------
#>
#> == Effect(s) (Both x-variable(s) and y-variable(s) Standardized) ==
#>
#> std CI.lo CI.hi Sig pvalue SE
#> x -> y 0.1245 -0.0816 0.3121 0.2264 0.1002
#>
#> - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#> nonparametric bootstrapping with 5000 samples.
#> - [pvalue] are asymmetric bootstrap p-values.
#> - [SE] are standard errors.
#> - std: The standardized effect(s).
#>
#> ===================================================
#> | Notes |
#> ===================================================
#>
#> - For reference, the bootstrap confidence interval (and bootstrap
#> p-value, if requested) of the (unstandardized) direct effect is also
#> reported. The bootstrap p-value and the OLS t-statistc p-value can be
#> different.
#> - For the direct effects with either 'x'-variable or 'y'-variable, or
#> both, standardized, it is recommended to use the bootstrap confidence
#> intervals, which take into account the sampling error of the sample
#> standard deviations.
#> - The asymmetric bootstrap value for an effect is the same whether x
#> and/or y is/are standardized.These are the main sections of the default results:
Basic Information
The variables, the models, and the number of cases. Listwise deletion is used and only cases without missing data on all variables in the models are used.
Regression Results
This part is simply the usual outputs of regression analysis
conducted by lm().
Indirect Effect Results
By default, this section prints the estimated indirect effects, confidence intervals, and asymmetric bootstrap p-values.
Four sections will be printed:
The original indirect effects.
The indirect effects with the predictor (“x”) standardized.
The indirect effects with the outcome (“y”) standardized.
The indirect effects with both the predictor (“x”) and the outcome (“y”) standardized, also called the completely standardized indirect effects or simply the standardized indirect effects.
These four versions of the results are printed by default such that users can select and interpret sections as they see fit.
Total Indirect Effect Results
By default, this section prints the estimated total indirect effects, confidence intervals, and asymmetric bootstrap p-values.
The total indirect effect in a parallel mediation model is the sum of all indirect effects from the predictor (“x”) to the outcome (“y”).
Four sections will be printed:
The original total indirect effect.
The total indirect effects with the predictor (“x”) standardized.
The total indirect effects with the outcome (“y”) standardized.
The total indirect effects with both the predictor (“x”) and the outcome (“y”) standardized, also called the completely standardized total indirect effects or simply the standardized total indirect effects.
These four versions of the results are printed by default such that users can select and interpret sections as they see fit.
Direct Effect Results
By default, this section prints the estimated direct effect (from the predictor “x” to the outcome “y”, not mediated), confidence interval, and asymmetric bootstrap p-value.
The OLS t-test of the direct effect is already available in section Regression Results. The bootstrap results are printed in case users prefer using the same confidence interval method for all the effects.
Additional Issues
Number of Mediators
Both q_serial_mediation() and
q_parallel_mediation() have no inherent limitation on the
number of mediators, other than that of stats::lm().
Customize Control Variables
If the control variables for the regress models are different, we can
set cov to a named list. The names are the variables with
control variables, and the element under each name is a character vector
of the control variables.
For example,
- If we set
covtolist(m1 = "c1", m2 = "c2", y = c("c1", "c2")), then onlyc1is included in predictingm1, onlyc2is included in predictingm2, while bothc1andc2are included in predictingy.
If this is a serial mediation model, then the three models are:
m1 ~ x + c1m2 ~ m1 + x + c2y ~ m1 + m2 + c1 + c2
A variable that does not appear in the list does not have control variables.
This is how the call to q_serial_mediation() should
be:
out_serial_v2 <- q_serial_mediation(x = "x",
y = "y",
m = c("m1", "m2"),
cov = list(m1 = "c1",
m2 = "c2",
y = c("c1", "c2")),
data = data_serial,
R = 5000,
seed = 1234)Customize The Printout
The print method of the output of the quick mediation
functions have arguments for customizing the output. These are arguments
that likely may be used:
digits: The number of digits after the decimal place for most reults. Default is 4.pvalue_digits: The number of digits after the decimal place for p-values. Default is 4.
See the help page of print.q_mediation() for other
arguments.
Speed and Parallel Processing
By default, parallel processing is used. If this failed for some
reasons, add parallel to FALSE. It will take
longer to run but should still be just one to two minutes in typical
models.
Progress Bar
BY default, a progress bar will be displayed when doing
bootstrapping. This can be disabled by adding
progress = FALSE.
Workflow
The quick functions are simply functions to do the following tasks internally:
Fit all the models by OLS regression using [stats::lm()].
Call
all_indirect_paths()to identify all indirect paths.Call
many_indirect_effects()to compute all indirect effects and form their confidence intervals.Call
total_indirect_effect()to compute the total indirect effect.
Therefore, all the tasks they do can be done manually by the functions above. These quick functions are developed just as convenient functions to do all these tasks in one call.
See this article for computing and testing indirect effects for more complicated models.
Final Remarks
For details on the quick functions, pleaes refer to the help page of
q_mediation().