Generate Monte Carlo Estimates

Introduction

This article is a brief illustration of how to use do_mc() from the package manymome (Cheung & Cheung, 2023) to generate Monte Carlo estimates for indirect_effect() and cond_indirect_effects() to form Monte Carlo confidence intervals.

Although indirect_effect() and cond_indirect_effects() can also be used to generate Monte Carlo estimates when they are called (see vignette("manymome")), there may be situations in which users prefer generating the Monte Carlo estimates first before calling indirect_effect() and cond_indirect_effects(). do_mc() is for this purpose.

Monte Carlo confidence intervals only support models fitted by lavaan::sem() and (since version 0.1.9.8) semTools::sem.mi() or semTools::runMI().

How It Works

The function do_mc() retrieves the variance-covariance matrix of the parameter estimates and then generates a number of sets of simulated sample estimates using a multivariate normal distribution. Other parameters and implied variances, covariances, and means of variables are then generated from these simulated estimates.

When a $(1 - \alpha)$ % Monte Carlo confidence interval is requested, the $100(\alpha/2)$ ^th percentile and the $100(1 - \alpha/2)$ ^th percentile are used to form the confidence interval. For a 95% Monte Carlo confidence interval, the 2.5^th percentile and 97.5^th percentile will be used.

The Workflow

The following workflow will be demonstrated;

Fit the model as usual.
Use do_mc() to generate the Monte Carlo estimates.
Call other functions (e.g, indirect_effect() and cond_indirect_effects()) to compute the desired effects and form Monte Carlo confidence intervals.

Demonstration

Fit a Model by `lavaan::sem()`

The data set for illustration:

library(manymome)
dat <- data_med
head(dat)
#>           x        m        y       c1       c2
#> 1  9.931992 17.89644 20.73893 1.426513 6.103290
#> 2  8.331493 17.92150 22.91594 2.940388 3.832698
#> 3 10.327471 17.83178 22.14201 3.012678 5.770532
#> 4 11.196969 20.01750 25.05038 3.120056 4.654931
#> 5 11.887811 22.08645 28.47312 4.440018 3.959033
#> 6  8.198297 16.95198 20.73549 2.495083 3.763712

It has one predictor (x), one mediator (m), one outcome variable (y), and two control variables (c1 and c2).

The following simple mediation model with two control variables (c1 and c2) will be fitted:

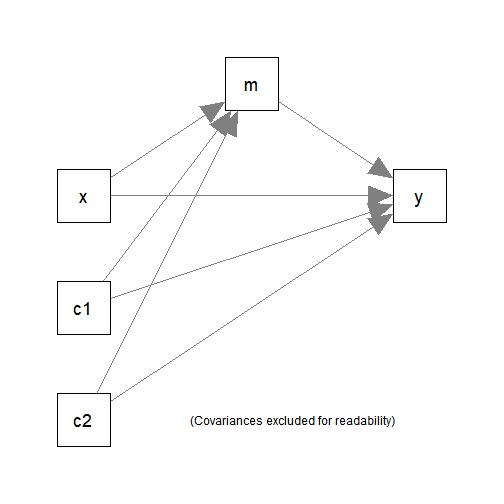
plot of chunk do_mc_draw_model

Fit the model by lavaan::sem():

mod <-
"
m ~ x + c1 + c2
y ~ m + x + c1 + c2
"
fit_lavaan <- sem(model = mod, data = dat,
                  fixed.x = FALSE,
                  estimator = "MLR")
summary(fit_lavaan)
#> lavaan 0.6-19 ended normally after 1 iteration
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        15
#> 
#>   Number of observations                           100
#> 
#> Model Test User Model:
#>                                               Standard      Scaled
#>   Test Statistic                                 0.000       0.000
#>   Degrees of freedom                                 0           0
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Sandwich
#>   Information bread                           Observed
#>   Observed information based on                Hessian
#> 
#> Regressions:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>   m ~                                                 
#>     x                 0.935    0.075   12.437    0.000
#>     c1                0.198    0.079    2.507    0.012
#>     c2               -0.168    0.099   -1.703    0.089
#>   y ~                                                 
#>     m                 0.785    0.233    3.363    0.001
#>     x                 0.508    0.323    1.573    0.116
#>     c1                0.140    0.188    0.747    0.455
#>     c2               -0.154    0.214   -0.720    0.471
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>   x ~~                                                
#>     c1                0.026    0.121    0.211    0.833
#>     c2                0.100    0.084    1.186    0.235
#>   c1 ~~                                               
#>     c2               -0.092    0.109   -0.841    0.400
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)
#>    .m                 0.681    0.085    7.976    0.000
#>    .y                 4.030    0.580    6.944    0.000
#>     x                 1.102    0.150    7.338    0.000
#>     c1                1.218    0.161    7.540    0.000
#>     c2                0.685    0.073    9.340    0.000

Suppose we would like to use robust “sandwich” standard errors and confidence intervals provided by MLR for the free parameters, but want to use Monte Carlo confidence interval for the indirect effect. In the call above, we used estimator = "MLR" and did not set se = "boot".

We can then call do_mc() on the output of lavaan::sem() to generate the Monte Carlo estimates of all free parameters and the implied statistics, such as the variances of m and y, which are not free parameters but are needed to form the confidence interval of the standardized indirect effect.

mc_out_lavaan <- do_mc(fit = fit_lavaan,
                       R = 10000,
                       seed = 4234)
#> Stage 1: Simulate estimates
#> Stage 2: Compute implied statistics

Usually, just three arguments are needed:

fit: The output of lavaan::sem().
R: The number of Monte Carlo replications. Should be at least 10000 in real research.
seed: The seed for the random number generator. To be used by set.seed(). It is recommended to set this argument such that the results are reproducible.

Parallel processing is not used. However, the time taken is rarely long because there is no need to refit the model many times.

Using the Output of `do_mc()` in Other Functions of `manymome`

When calling indirect_effect() or cond_indirect_effects(), the argument mc_out can be assigned the output of do_mc(). They will then retrieve the stored simulated estimates to form the Monte Carlo confidence intervals, if requested.

out_lavaan <- indirect_effect(x = "x",
                              y = "y",
                              m = "m",
                              fit = fit_lavaan,
                              mc_ci = TRUE,
                              mc_out = mc_out_lavaan)
out_lavaan
#> 
#> == Indirect Effect  ==
#>                                        
#>  Path:                 x -> m -> y     
#>  Indirect Effect:      0.733           
#>  95.0% Monte Carlo CI: [0.301 to 1.180]
#> 
#> Computation Formula:
#>   (b.m~x)*(b.y~m)
#> 
#> Computation:
#>   (0.93469)*(0.78469)
#> 
#> 
#> Monte Carlo confidence interval with 10000 replications.
#> 
#> Coefficients of Component Paths:
#>  Path Coefficient
#>   m~x       0.935
#>   y~m       0.785

Reusing the simulated estimates can ensure that all analyses with Monte Carlo confidence intervals are based on the same set of simulated estimates, without the need to generate these estimates again.

Missing Data

Monte Carlo confidence intervals can be formed when the variance-covariance matrix of the parameter estimates can be retrieved. Therefore, do_mc() can be used when missing data is handled by full information maximum likelihood in lavaan using missing = "fiml". It also supports multiple imputation if semTools::sem.mi() or semTools::runMI() (since version 0.1.9.8). See vignette("do_mc_lavaan_mi") for an illustration.

The Structure of the Output

The output of do_mc() in this case is an object of the class mc_out, which is a list of R lists, each with two elements: est and implied_stats.

This is the content of est of the first list:

mc_out_lavaan[[1]]$est
#>    lhs op rhs    est
#> 1    m  ~   x  0.909
#> 2    m  ~  c1  0.198
#> 3    m  ~  c2 -0.163
#> 4    y  ~   m  0.641
#> 5    y  ~   x  0.921
#> 6    y  ~  c1  0.010
#> 7    y  ~  c2  0.141
#> 8    m ~~   m  0.641
#> 9    y ~~   y  3.432
#> 10   x ~~   x  1.023
#> 11   x ~~  c1  0.074
#> 12   x ~~  c2  0.028
#> 13  c1 ~~  c1  1.180
#> 14  c1 ~~  c2 -0.261
#> 15  c2 ~~  c2  0.718

The content is just the first four columns of the output of lavaan::parameterEstimates(). Note that only fixed and free parameters are used so other rows, if any, are not used even if present.

This is the content of implied_stats of the first list:

mc_out_lavaan[[1]]$implied_stats
#> $cov
#>         m      y      x     c1     c2
#> m   1.586                            
#> y   1.864  6.059                     
#> x   0.939  1.548  1.023              
#> c1  0.344  0.263  0.074  1.180       
#> c2 -0.143  0.033  0.028 -0.261  0.718
#> 
#> $mean
#>  m  y  x c1 c2 
#> NA NA NA NA NA

It has three elements. cov is the implied variances and covariances of all variables. If a model has latent variables, they will be included too. The other elements, mean and mean_lv, are the implied means of the observed variables and the latent variables (if any), respectively. The elements are NA if mean structure is not in the fitted model.

Limitations

Monte Carlo confidence intervals require the variance-covariance matrix of all free parameters. Therefore, only models fitted by lavaan::sem() and (since 0.1.9.8) semTools::sem.mi() or semTools::runMI() are supported. Models fitted by stats::lm() do not have a variance-covariance matrix for the regression coefficients from two or more regression models and so are not supported by do_mc().

Further Information

For further information on do_mc(), please refer to its help page.

Reference

Cheung, S. F., & Cheung, S.-H. (2023). manymome: An R package for computing the indirect effects, conditional effects, and conditional indirect effects, standardized or unstandardized, and their bootstrap confidence intervals, in many (though not all) models. Behavior Research Methods. https://doi.org/10.3758/s13428-023-02224-z