Mediation Analysis by Multiple Regression

Introduction

This article is a brief illustration of how to use indirect_effect() from the package manymome (Cheung & Cheung, 2023) to estimate the indirect effects when the model parameters are estimated by ordinary least squares (OLS) multiple regression using lm().

Data Set and Model

This is the sample dataset used for illustration:

library(manymome)
dat <- data_med_complicated
print(round(head(dat), 2))
#>      x1   x2  m11  m12   m2   y1    y2   c1    c2
#> 1 10.16 4.00 5.84 6.78 7.11 6.06 10.38 5.01  8.20
#> 2 10.89 4.79 4.95 5.81 7.92 5.15  8.52 3.92  9.90
#> 3  9.99 5.79 4.95 4.47 8.21 3.25  7.81 5.91 11.36
#> 4 12.36 4.80 5.56 6.21 8.88 6.27  9.41 6.06 10.49
#> 5 10.85 6.39 6.19 5.39 8.76 5.36  9.84 4.28  9.81
#> 6 10.28 4.58 4.88 4.28 8.50 4.57 10.42 4.71 11.38

This dataset has 9 variables: 2 predictors (x1 and x2), three mediators (m11, m12, and m2), two outcome variables (y1 and y2), and two control variables (c1 and c2).

Suppose this is the model to be fitted:

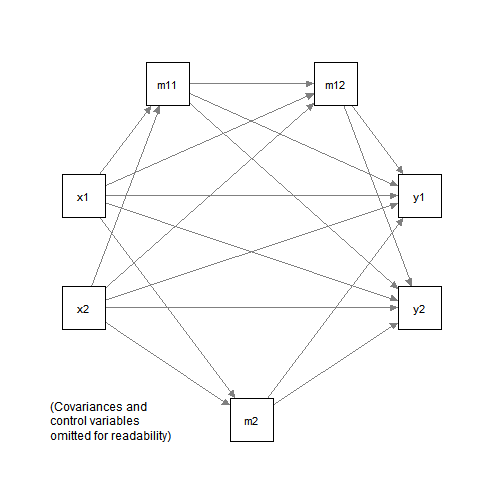
plot of chunk med_lm_draw_model

Despite the apparent complexity, the path parameters can be estimated by five multiple regression models:

lm_m11 <- lm(m11 ~ x1 + x2 + c1 + c2, dat)
lm_m12 <- lm(m12 ~ m11 + x1 + x2 + c1 + c2, dat)
lm_m2 <- lm(m2 ~ x1 + x2 + c1 + c2, dat)
lm_y1 <- lm(y1 ~ m12 + m2 + m11 + x1 + x2 + c1 + c2, dat)
lm_y2 <- lm(y2 ~ m12 + m2 + m11 + x1 + x2 + c1 + c2, dat)

These are the regression coefficient estimates of the paths (those of control variables omitted):

#>        m11    m12    m2     y1     y2
#> x1   0.352 -0.212 0.022 -0.078  0.115
#> x2  -0.045 -0.072 0.289  0.003  0.062
#> m11         0.454        0.147  0.024
#> m12                      0.234  0.135
#> m2                      -0.433 -0.436

Although not mandatory, it is recommended to combine these five models into one object (a system of regression models) using lm2list():

fit_lm <- lm2list(lm_m11, lm_m12, lm_m2, lm_y1, lm_y2)
fit_lm
#> 
#> The model(s):
#> m11 ~ x1 + x2 + c1 + c2
#> m12 ~ m11 + x1 + x2 + c1 + c2
#> m2 ~ x1 + x2 + c1 + c2
#> y1 ~ m12 + m2 + m11 + x1 + x2 + c1 + c2
#> y2 ~ m12 + m2 + m11 + x1 + x2 + c1 + c2

Simply use the lm() outputs as arguments. Order does not matter. To ensure that the regression outputs can be validly combined, lm2list() will also check:

whether the same sample is used in all regression analysis (not just same sample size, but the same set of cases), and
whether the models are “connected”, to ensure that the regression outputs can be validly combined.

Generating Bootstrap Estimates

To form nonparametric bootstrap confidence interval for indirect effects to be computed, do_boot() can be used to generate bootstrap estimates for all regression coefficients first. These estimates can be reused for any indirect effects to be estimated.

boot_out_lm <- do_boot(fit_lm,
                       R = 100,
                       seed = 54532,
                       ncores = 1)

Please see vignette("do_boot") or the help page of do_boot() on how to use this function. In real research, R, the number of bootstrap samples, should be set to 2000 or even 5000. The argument ncores can usually be omitted unless users want to manually control the number of CPU cores used in parallel processing.

Indirect Effects

We can now use indirect_effect() to estimate the indirect effect and form its bootstrap confidence interval for any path in the model. By reusing the generated bootstrap estimates, there is no need to repeat the resampling.

Suppose we want to estimate the indirect effect from x1 to y1 through m11 and m12:

(Refer to vignette("manymome") and the help page of indirect_effect() on the arguments.)

out_x1m11m12y1 <- indirect_effect(x = "x1",
                                  y = "y1",
                                  m = c("m11", "m12"),
                                  fit = fit_lm,
                                  boot_ci = TRUE,
                                  boot_out = boot_out_lm)
out_x1m11m12y1
#> 
#> == Indirect Effect  ==
#>                                            
#>  Path:               x1 -> m11 -> m12 -> y1
#>  Indirect Effect:    0.037                 
#>  95.0% Bootstrap CI: [0.003 to 0.077]      
#> 
#> Computation Formula:
#>   (b.m11~x1)*(b.m12~m11)*(b.y1~m12)
#> 
#> Computation:
#>   (0.35204)*(0.45408)*(0.23402)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>     Path Coefficient
#>   m11~x1       0.352
#>  m12~m11       0.454
#>   y1~m12       0.234

The indirect effect is 0.037, with 95% confidence interval [0.003, 0.077].

Similarly, we can estimate the indirect effect from x2 to y2 through m2:

out_x2m2y2 <- indirect_effect(x = "x2",
                              y = "y2",
                              m = "m2",
                              fit = fit_lm,
                              boot_ci = TRUE,
                              boot_out = boot_out_lm)
out_x2m2y2
#> 
#> == Indirect Effect  ==
#>                                        
#>  Path:               x2 -> m2 -> y2    
#>  Indirect Effect:    -0.126            
#>  95.0% Bootstrap CI: [-0.233 to -0.043]
#> 
#> Computation Formula:
#>   (b.m2~x2)*(b.y2~m2)
#> 
#> Computation:
#>   (0.28901)*(-0.43598)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>   Path Coefficient
#>  m2~x2       0.289
#>  y2~m2      -0.436

The indirect effect is -0.126, with 95% confidence interval [-0.233, -0.043].

Note that any indirect path in the model can be estimated this way. Suppose, after doing the regression analysis, we want to estimate the indirect effect from x2 to m12 through m11, we just call indirect_effect():

out_x2m11m12 <- indirect_effect(x = "x2",
                                y = "m12",
                                m = "m11",
                                fit = fit_lm,
                                boot_ci = TRUE,
                                boot_out = boot_out_lm)
out_x2m11m12
#> 
#> == Indirect Effect  ==
#>                                       
#>  Path:               x2 -> m11 -> m12 
#>  Indirect Effect:    -0.020           
#>  95.0% Bootstrap CI: [-0.139 to 0.110]
#> 
#> Computation Formula:
#>   (b.m11~x2)*(b.m12~m11)
#> 
#> Computation:
#>   (-0.04471)*(0.45408)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>     Path Coefficient
#>   m11~x2     -0.0447
#>  m12~m11      0.4541

The indirect effect is -0.020, with 95% confidence interval [-0.139, 0.110].

There is no limit on the path to be estimated, as long as all required path coefficients are in the model. indirect_effect() will also check whether a path is valid. Therefore, estimating the effect from x1 to m2 through m11 will result in an error because this path does not exist in the model defined by the regression outputs.

Standardized Indirect effects

The standardized indirect effect from x1 to y1 through m11 and m12 can be estimated by setting standardized_x and standardized_y to `TRUE:

std_x1m11m12y1 <- indirect_effect(x = "x1",
                                  y = "y1",
                                  m = c("m11", "m12"),
                                  fit = fit_lm,
                                  boot_ci = TRUE,
                                  boot_out = boot_out_lm,
                                  standardized_x = TRUE,
                                  standardized_y = TRUE)
std_x1m11m12y1
#> 
#> == Indirect Effect (Both 'x1' and 'y1' Standardized) ==
#>                                            
#>  Path:               x1 -> m11 -> m12 -> y1
#>  Indirect Effect:    0.039                 
#>  95.0% Bootstrap CI: [0.004 to 0.085]      
#> 
#> Computation Formula:
#>   (b.m11~x1)*(b.m12~m11)*(b.y1~m12)*sd_x1/sd_y1
#> 
#> Computation:
#>   (0.35204)*(0.45408)*(0.23402)*(1.11605)/(1.06579)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>     Path Coefficient
#>   m11~x1       0.352
#>  m12~m11       0.454
#>   y1~m12       0.234
#> 
#> NOTE:
#> - The effects of the component paths are from the model, not
#>   standardized.

The standardized indirect effect is 0.039, with 95% confidence interval [0.004,0.085].

Similarly, we can estimate the standardized indirect effect from x1 to y1 through m2:

std_x1m2y1 <- indirect_effect(x = "x1",
                              y = "y1",
                              m = "m2",
                              fit = fit_lm,
                              boot_ci = TRUE,
                              boot_out = boot_out_lm,
                              standardized_x = TRUE,
                              standardized_y = TRUE)
std_x1m2y1
#> 
#> == Indirect Effect (Both 'x1' and 'y1' Standardized) ==
#>                                       
#>  Path:               x1 -> m2 -> y1   
#>  Indirect Effect:    -0.010           
#>  95.0% Bootstrap CI: [-0.069 to 0.067]
#> 
#> Computation Formula:
#>   (b.m2~x1)*(b.y1~m2)*sd_x1/sd_y1
#> 
#> Computation:
#>   (0.02233)*(-0.43300)*(1.11605)/(1.06579)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>   Path Coefficient
#>  m2~x1      0.0223
#>  y1~m2     -0.4330
#> 
#> NOTE:
#> - The effects of the component paths are from the model, not
#>   standardized.

The standardized indirect effect is -0.010, with 95% confidence interval [-0.069, 0.067].

Adding Effects

Note that the results of indirect_effect() can be added using +.

For example, to find the total indirect effect of x1 on y1, we need to compute the indirect effects along the following paths:

x1 to m11 to m12 to y1
x1 to m11 to y1
x1 to m12 to y1
x1 to m2 to y1

The indirect effects along Path a has already been computed. We compute the indirect effects along Paths b, c, and d below:

out_x1m11y1 <- indirect_effect(x = "x1",
                               y = "y1",
                               m = "m11",
                               fit = fit_lm,
                               boot_ci = TRUE,
                               boot_out = boot_out_lm)
out_x1m11y1
#> 
#> == Indirect Effect  ==
#>                                       
#>  Path:               x1 -> m11 -> y1  
#>  Indirect Effect:    0.052            
#>  95.0% Bootstrap CI: [-0.036 to 0.103]
#> 
#> Computation Formula:
#>   (b.m11~x1)*(b.y1~m11)
#> 
#> Computation:
#>   (0.35204)*(0.14694)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>    Path Coefficient
#>  m11~x1       0.352
#>  y1~m11       0.147

out_x1m12y1 <- indirect_effect(x = "x1",
                               y = "y1",
                               m = "m12",
                               fit = fit_lm,
                               boot_ci = TRUE,
                               boot_out = boot_out_lm)
out_x1m12y1
#> 
#> == Indirect Effect  ==
#>                                        
#>  Path:               x1 -> m12 -> y1   
#>  Indirect Effect:    -0.050            
#>  95.0% Bootstrap CI: [-0.125 to -0.000]
#> 
#> Computation Formula:
#>   (b.m12~x1)*(b.y1~m12)
#> 
#> Computation:
#>   (-0.21182)*(0.23402)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>    Path Coefficient
#>  m12~x1      -0.212
#>  y1~m12       0.234

out_x1m2y1 <- indirect_effect(x = "x1",
                               y = "y1",
                               m = "m2",
                               fit = fit_lm,
                               boot_ci = TRUE,
                               boot_out = boot_out_lm)
out_x1m2y1
#> 
#> == Indirect Effect  ==
#>                                       
#>  Path:               x1 -> m2 -> y1   
#>  Indirect Effect:    -0.010           
#>  95.0% Bootstrap CI: [-0.077 to 0.064]
#> 
#> Computation Formula:
#>   (b.m2~x1)*(b.y1~m2)
#> 
#> Computation:
#>   (0.02233)*(-0.43300)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>   Path Coefficient
#>  m2~x1      0.0223
#>  y1~m2     -0.4330

We can now compute the total indirect effect:

out_x1y1_total <- out_x1m11m12y1 + out_x1m11y1 + out_x1m12y1 + out_x1m2y1
out_x1y1_total
#> 
#> == Indirect Effect  ==
#>                                             
#>  Path:                x1 -> m11 -> m12 -> y1
#>  Path:                x1 -> m11 -> y1       
#>  Path:                x1 -> m12 -> y1       
#>  Path:                x1 -> m2 -> y1        
#>  Function of Effects: 0.030                 
#>  95.0% Bootstrap CI:  [-0.088 to 0.132]     
#> 
#> Computation of the Function of Effects:
#>  (((x1->m11->m12->y1)
#> +(x1->m11->y1))
#> +(x1->m12->y1))
#> +(x1->m2->y1) 
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.

The total effect of f1 on f4 is 0.030, with 95% confidence interval [-0.088, 0.132].

See help("math_indirect") for further details on addition for indirect_effect() outputs.

Differences in Effects

Subtraction can also be conducted using -. For example, we can compute the difference between the indirect effect of x1 on y1 through m11 and m12 and the indirect effect of x1 on y1 through m2:

out_x1_diff <- out_x1m11m12y1 - out_x1m2y1
out_x1_diff
#> 
#> == Indirect Effect  ==
#>                                             
#>  Path:                x1 -> m11 -> m12 -> y1
#>  Path:                x1 -> m2 -> y1        
#>  Function of Effects: 0.047                 
#>  95.0% Bootstrap CI:  [-0.038 to 0.118]     
#> 
#> Computation of the Function of Effects:
#>  (x1->m11->m12->y1)
#> -(x1->m2->y1) 
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.

The difference in effects is 0.047, with 95% confidence interval [-0.038, 0.118].

See help("math_indirect") for further details on subtraction for indirect_effect() outputs.

Identifying All Indirect paths

If there are several indirect paths in a model, the function all_indirect_paths() can be used to automatically identify all indirect paths (a path with at least one mediator) in a model:

all_paths <- all_indirect_paths(fit = fit_lm)
all_paths
#> Call: 
#> all_indirect_paths(fit = fit_lm)
#> Path(s): 
#>    path                  
#> 1  m11 -> m12 -> y1      
#> 2  m11 -> m12 -> y2      
#> 3  x1 -> m11 -> m12      
#> 4  x1 -> m11 -> m12 -> y1
#> 5  x1 -> m11 -> y1       
#> 6  x1 -> m12 -> y1       
#> 7  x1 -> m2 -> y1        
#> 8  x1 -> m11 -> m12 -> y2
#> 9  x1 -> m11 -> y2       
#> 10 x1 -> m12 -> y2       
#> 11 x1 -> m2 -> y2        
#> 12 x2 -> m11 -> m12      
#> 13 x2 -> m11 -> m12 -> y1
#> 14 x2 -> m11 -> y1       
#> 15 x2 -> m12 -> y1       
#> 16 x2 -> m2 -> y1        
#> 17 x2 -> m11 -> m12 -> y2
#> 18 x2 -> m11 -> y2       
#> 19 x2 -> m12 -> y2       
#> 20 x2 -> m2 -> y2        
#> 21 c1 -> m11 -> m12      
#> 22 c1 -> m11 -> m12 -> y1
#> 23 c1 -> m11 -> y1       
#> 24 c1 -> m12 -> y1       
#> 25 c1 -> m2 -> y1        
#> 26 c1 -> m11 -> m12 -> y2
#> 27 c1 -> m11 -> y2       
#> 28 c1 -> m12 -> y2       
#> 29 c1 -> m2 -> y2        
#> 30 c2 -> m11 -> m12      
#> 31 c2 -> m11 -> m12 -> y1
#> 32 c2 -> m11 -> y1       
#> 33 c2 -> m12 -> y1       
#> 34 c2 -> m2 -> y1        
#> 35 c2 -> m11 -> m12 -> y2
#> 36 c2 -> m11 -> y2       
#> 37 c2 -> m12 -> y2       
#> 38 c2 -> m2 -> y2

The initial list is very long because control variables (c1 and c2) are included in the search. Moreover, paths that start from a mediator or end at a mediator are also included. Users can customize the search:

all_paths <- all_indirect_paths(fit = fit_lm,
                                x = c("x1", "x2"),
                                y = c("y1", "y2"),
                                exclude = c("c1", "c2"))
all_paths
#> Call: 
#> all_indirect_paths(fit = fit_lm, exclude = c("c1", "c2"), x = c("x1", 
#>     "x2"), y = c("y1", "y2"))
#> Path(s): 
#>    path                  
#> 1  x1 -> m11 -> m12 -> y1
#> 2  x1 -> m11 -> y1       
#> 3  x1 -> m12 -> y1       
#> 4  x1 -> m2 -> y1        
#> 5  x1 -> m11 -> m12 -> y2
#> 6  x1 -> m11 -> y2       
#> 7  x1 -> m12 -> y2       
#> 8  x1 -> m2 -> y2        
#> 9  x2 -> m11 -> m12 -> y1
#> 10 x2 -> m11 -> y1       
#> 11 x2 -> m12 -> y1       
#> 12 x2 -> m2 -> y1        
#> 13 x2 -> m11 -> m12 -> y2
#> 14 x2 -> m11 -> y2       
#> 15 x2 -> m12 -> y2       
#> 16 x2 -> m2 -> y2

x is a vector of names. Only paths start from these variables will be included.
y is a vector of names. Only paths end at these variables will be included.
exclude is a vector of names. Paths that involve these variables will be excluded.

The output is a all_paths-class object. It can be used in many_indirect_effects()

out_all <- many_indirect_effects(paths = all_paths,
                                 fit = fit_lm,
                                 boot_ci = TRUE,
                                 boot_out = boot_out_lm)

The first argument, paths, is the output of all_indirect_paths(). The other arguments will be passed to indirect_effect().

The output is an indirect_list-class object, which is a list of the outputs of indirect_effects(). If printed, a summary of the indirect effects will be printed:

out_all
#> 
#> ==  Indirect Effect(s)   ==
#>                           ind  CI.lo  CI.hi Sig
#> x1 -> m11 -> m12 -> y1  0.037  0.003  0.077 Sig
#> x1 -> m11 -> y1         0.052 -0.036  0.103    
#> x1 -> m12 -> y1        -0.050 -0.125 -0.000 Sig
#> x1 -> m2 -> y1         -0.010 -0.077  0.064    
#> x1 -> m11 -> m12 -> y2  0.022 -0.015  0.065    
#> x1 -> m11 -> y2         0.009 -0.086  0.093    
#> x1 -> m12 -> y2        -0.029 -0.089  0.014    
#> x1 -> m2 -> y2         -0.010 -0.074  0.068    
#> x2 -> m11 -> m12 -> y1 -0.005 -0.044  0.017    
#> x2 -> m11 -> y1        -0.007 -0.055  0.034    
#> x2 -> m12 -> y1        -0.017 -0.054  0.049    
#> x2 -> m2 -> y1         -0.125 -0.258 -0.031 Sig
#> x2 -> m11 -> m12 -> y2 -0.003 -0.021  0.022    
#> x2 -> m11 -> y2        -0.001 -0.021  0.052    
#> x2 -> m12 -> y2        -0.010 -0.056  0.045    
#> x2 -> m2 -> y2         -0.126 -0.233 -0.043 Sig
#> 
#>  - [CI.lo to CI.hi] are 95.0% percentile confidence intervals by
#>    nonparametric bootstrapping with 100 samples.
#>  - The 'ind' column shows the indirect effects.
#>

The output of many_indirect_effects() is a named list, names being the path name as appeared in the output. Individual indirect effects can be extracted using either the indices or the path names

An example using index:

out1 <- out_all[[1]]
out1
#> 
#> == Indirect Effect  ==
#>                                            
#>  Path:               x1 -> m11 -> m12 -> y1
#>  Indirect Effect:    0.037                 
#>  95.0% Bootstrap CI: [0.003 to 0.077]      
#> 
#> Computation Formula:
#>   (b.m11~x1)*(b.m12~m11)*(b.y1~m12)
#> 
#> Computation:
#>   (0.35204)*(0.45408)*(0.23402)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>     Path Coefficient
#>   m11~x1       0.352
#>  m12~m11       0.454
#>   y1~m12       0.234

An example using path name (though not recommended because the name is usually long):

out2 <- out_all[["x2 -> m2 -> y2"]]
out2
#> 
#> == Indirect Effect  ==
#>                                        
#>  Path:               x2 -> m2 -> y2    
#>  Indirect Effect:    -0.126            
#>  95.0% Bootstrap CI: [-0.233 to -0.043]
#> 
#> Computation Formula:
#>   (b.m2~x2)*(b.y2~m2)
#> 
#> Computation:
#>   (0.28901)*(-0.43598)
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.
#> 
#> Coefficients of Component Paths:
#>   Path Coefficient
#>  m2~x2       0.289
#>  y2~m2      -0.436

The extracted element can be used just like the outputs of indirect_effect() in previous section.

See the help page of all_indirect_paths() and many_indirect_effects() for other arguments available.

Total Indirect Effect

The total indirect effect between two variables in a list of paths can be computed by total_indirect_effect().

total_x1_y1 <- total_indirect_effect(out_all,
                                     x = "x1",
                                     y = "y1")
total_x1_y1
#> 
#> == Indirect Effect  ==
#>                                             
#>  Path:                x1 -> m11 -> m12 -> y1
#>  Path:                x1 -> m11 -> y1       
#>  Path:                x1 -> m12 -> y1       
#>  Path:                x1 -> m2 -> y1        
#>  Function of Effects: 0.030                 
#>  95.0% Bootstrap CI:  [-0.088 to 0.132]     
#> 
#> Computation of the Function of Effects:
#>  (((x1->m11->m12->y1)
#> +(x1->m11->y1))
#> +(x1->m12->y1))
#> +(x1->m2->y1) 
#> 
#> 
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 100 bootstrap samples.

The first argument is the output of many_indirect_effects() or a list of indirect-class object. x is the name of the variable that starts the paths. y is the name of the variable that ends the paths.

Further Information

For further information on do_boot() and indirect_effect(), please refer to their help pages.

Reference

Cheung, S. F., & Cheung, S.-H. (2023). manymome: An R package for computing the indirect effects, conditional effects, and conditional indirect effects, standardized or unstandardized, and their bootstrap confidence intervals, in many (though not all) models. Behavior Research Methods. https://doi.org/10.3758/s13428-023-02224-z

Shu Fai Cheung & Sing-Hang Cheung

2024-10-04