Generate Bootstrap Estimates
Shu Fai Cheung & Sing-Hang Cheung
2025-08-10
Source:vignettes/do_boot.Rmd
do_boot.RmdIntroduction
This article is a brief illustration of how to use
do_boot() from the package manymome (Cheung & Cheung,
2024) to generate bootstrap estimates for
indirect_effect() and cond_indirect_effects()
to form bootstrap confidence intervals.
Although indirect_effect() and
cond_indirect_effects() can also be used to generate
bootstrap estimates when they are called (see
vignette("manymome")), there may be situations in which
users prefer generating the bootstrap estimates first before calling
indirect_effect() and cond_indirect_effects().
do_boot() is for this purpose.
The Workflow
The following workflow will be demonstrated;
Fit the model as usual.
Use
do_boot()to generate the bootstrap estimates.Call other functions (e.g,
indirect_effect()andcond_indirect_effects()) to compute the desired effects and form bootstrap confidence intervals.
Demonstration: lavaan::sem()
Fit a Model by lavaan::sem()
The data set for illustration:
library(manymome)
dat <- data_med
head(dat)
#> x m y c1 c2
#> 1 9.931992 17.89644 20.73893 1.426513 6.103290
#> 2 8.331493 17.92150 22.91594 2.940388 3.832698
#> 3 10.327471 17.83178 22.14201 3.012678 5.770532
#> 4 11.196969 20.01750 25.05038 3.120056 4.654931
#> 5 11.887811 22.08645 28.47312 4.440018 3.959033
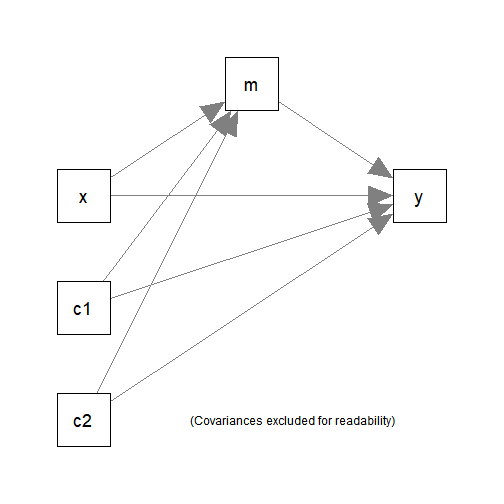
#> 6 8.198297 16.95198 20.73549 2.495083 3.763712It has one predictor (x), one mediator (m),
one outcome variable (y), and two control variables
(c1 and c2).
This simple mediation model with two control variables
(c1 and c2) will be fitted:
We first fit the model by lavaan::sem():
mod <-
"
m ~ x + c1 + c2
y ~ m + x + c1 + c2
"
fit_lavaan <- sem(model = mod, data = dat,
fixed.x = FALSE,
estimator = "MLR")
summary(fit_lavaan)
#> lavaan 0.6-19 ended normally after 1 iteration
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 15
#>
#> Number of observations 100
#>
#> Model Test User Model:
#> Standard Scaled
#> Test Statistic 0.000 0.000
#> Degrees of freedom 0 0
#>
#> Parameter Estimates:
#>
#> Standard errors Sandwich
#> Information bread Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> m ~
#> x 0.935 0.075 12.437 0.000
#> c1 0.198 0.079 2.507 0.012
#> c2 -0.168 0.099 -1.703 0.089
#> y ~
#> m 0.785 0.233 3.363 0.001
#> x 0.508 0.323 1.573 0.116
#> c1 0.140 0.188 0.747 0.455
#> c2 -0.154 0.214 -0.720 0.471
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> x ~~
#> c1 0.026 0.121 0.211 0.833
#> c2 0.100 0.084 1.186 0.235
#> c1 ~~
#> c2 -0.092 0.109 -0.841 0.400
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .m 0.681 0.085 7.976 0.000
#> .y 4.030 0.580 6.944 0.000
#> x 1.102 0.150 7.338 0.000
#> c1 1.218 0.161 7.540 0.000
#> c2 0.685 0.073 9.340 0.000Suppose we would like to use robust “sandwich” standard errors and
confidence intervals provided by MLR for the free parameters, but want
to use percentile nonparametric bootstrap confidence interval for the
indirect effect. In the call above, we used
estimator = "MLR" and did not set
se = "boot".
Generate Bootstrap Estimates
We can then call do_boot() on the output of
lavaan::sem() to generate the bootstrap estimates of all
free parameters and the implied statistics, such as the
variances of m and y, which are not free
parameters but are needed to form the confidence interval of the
standardized indirect effect.
boot_out_lavaan <- do_boot(fit = fit_lavaan,
R = 500,
ncores = 1,
seed = 58491)Usually, just three arguments are needed:
fit: The output oflavaan::sem().R: The number of bootstrap samples. Should be at least 2000 or even 5000 in real research. 500 is used here just for illustration.ncores: The number of CPU cores to be used in generating bootstrap estimates in parallel processing.seed: The seed for the random number generator. To be used byset.seed(). It is recommended to set this argument such that the results are reproducible.
Parallel processing is enabled by default, and a text progress bar
(generated by the package pbapply) will be displayed. If
ncores is omitted, the number of cores
(ncores) to be used will be decided automatically.
Therefore, users usually do not need to use ncores. It is
set to 1 here just for illustration.
In real research with a complicated model and moderate to large
sample size, even with parallel processing, it may take several minutes,
or even over twenty minutes in some cases. Nevertheless, this only need
to be conducted once in the workflow of manymome.
If bootstrapping takes an appreciable time to run, it is recommended
to save the output using saveRDS() or
save():
### Use saveRDS() ###
# Save the output
saveRDS(boot_out_lavaan, file = "boot_out_lavaan.rds")
# Load the output
boot_out_lavaan <- readRDS("boot_out_lavaan.rds")
### Use save() ###
# Save the output
save(boot_out_lavaan, file = "boot_out_lavaan.RData")
# Load the output
load("boot_out_lavaan.RData")We recommend readRDS() although save() is
probably a more popular function.
Using the Output of do_boot() in Other Functions of
manymome
When calling indirect_effect() or
cond_indirect_effects(), the argument boot_out
can be assigned the output of do_bout(). They will then
retrieve he stored bootstrap estimates to form the percentile bootstrap
confidence intervals, if requested.
out_lavaan <- indirect_effect(x = "x",
y = "y",
m = "m",
fit = fit_lavaan,
boot_ci = TRUE,
boot_out = boot_out_lavaan)
out_lavaan
#>
#> == Indirect Effect ==
#>
#> Path: x -> m -> y
#> Indirect Effect: 0.733
#> 95.0% Bootstrap CI: [0.270 to 1.228]
#>
#> Computation Formula:
#> (b.m~x)*(b.y~m)
#>
#> Computation:
#> (0.93469)*(0.78469)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#>
#> Coefficients of Component Paths:
#> Path Coefficient
#> m~x 0.935
#> y~m 0.785Reusing the bootstrap estimates can ensure that all analysis with bootstrap confidence intervals are based on the same set of bootstrap samples.
The function also supports bias-corrected (BC) confidence interval,
which can be requested by adding boot_type = "bc" to the
call of indirect_effect(). However, authors in some recent
work do not advocate this method (e.g., Falk & Biesanz, 2015; Hayes,
2022; Tofighi & Kelley, 2020). Therefore, this option is provided
merely for research purpose.
Demonstration: lm()
Fit the Model by Several Calls to lm()
Suppose we estimate the parameters using multiple regression. We need
to fit two regression models, one predicts m and the other
predicts y:
# Fit Models
lm_m <- lm(m ~ x + c1 + c2, dat)
lm_y <- lm(y ~ m + x + c1 + c2, dat)
#
# ###### Regression: Predict m ######
summary(lm_m)
#>
#> Call:
#> lm(formula = m ~ x + c1 + c2, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.82810 -0.56016 -0.08481 0.52524 2.09155
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 9.68941 0.91979 10.534 <2e-16 ***
#> x 0.93469 0.08083 11.563 <2e-16 ***
#> c1 0.19778 0.07678 2.576 0.0115 *
#> c2 -0.16841 0.10305 -1.634 0.1055
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.8425 on 96 degrees of freedom
#> Multiple R-squared: 0.5981, Adjusted R-squared: 0.5855
#> F-statistic: 47.62 on 3 and 96 DF, p-value: < 2.2e-16
#
# ###### Regression: Predict y ######
#
summary(lm_y)
#>
#> Call:
#> lm(formula = y ~ m + x + c1 + c2, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1336 -1.3365 -0.1014 1.4597 6.5470
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.4152 3.3016 1.337 0.18432
#> m 0.7847 0.2495 3.145 0.00222 **
#> x 0.5077 0.3057 1.661 0.10004
#> c1 0.1405 0.1941 0.724 0.47093
#> c2 -0.1544 0.2554 -0.604 0.54695
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.06 on 95 degrees of freedom
#> Multiple R-squared: 0.3576, Adjusted R-squared: 0.3305
#> F-statistic: 13.22 on 4 and 95 DF, p-value: 1.336e-08To use do_boot(), we first combine the regression
outputs to one object using lm2list(). The output is an
lm_list-class object.
fit_lm <- lm2list(lm_m, lm_y)
fit_lm
#>
#> The model(s):
#> m ~ x + c1 + c2
#> y ~ m + x + c1 + c2Generate Bootstrap Estimates
We can now use do_boot() as described above, using the
output of lm2list() instead of the output of
lavaan::sem():
boot_out_lm <- do_boot(fit = fit_lm,
R = 500,
seed = 98715,
ncores = 1)Like working on the outputs of lavaan::lavaan(),
parallel processing is also used by default. ncores is the
number of CPU cores to be used. Because the output may not be saved, it
is recommended to set the seed of the random number generation using
seed, set to 98715 in the above example. The seed can be
any integer within the range allowed in R, see set.seed().
Setting the seed ensures that the same R set of bootstrap
samples will be generated every time.
Using the Output of do_boot() in Other Functions of
manymome
When calling indirect_effect() or
cond_indirect_effects(), we cab set the argument
boot_out to the output of do_bout():
out_lm <- indirect_effect(x = "x",
y = "y",
m = "m",
fit = fit_lm,
boot_ci = TRUE,
boot_out = boot_out_lm)
out_lm
#>
#> == Indirect Effect ==
#>
#> Path: x -> m -> y
#> Indirect Effect: 0.733
#> 95.0% Bootstrap CI: [0.292 to 1.201]
#>
#> Computation Formula:
#> (b.m~x)*(b.y~m)
#>
#> Computation:
#> (0.93469)*(0.78469)
#>
#>
#> Percentile confidence interval formed by nonparametric bootstrapping
#> with 500 bootstrap samples.
#>
#> Coefficients of Component Paths:
#> Path Coefficient
#> m~x 0.935
#> y~m 0.785As long as users are aware of the potential problem with
bias-corrected (BC) bootstrap confidence interval (see the references
cited above), boot_type = "bc" can be used to request BC
bootstrap confidence interval instead of the default percentile
bootstrap confidence interval.
The Structure of the Output
Models Fitted by lavaan::sem()
The output of do_boot() in this case is an object of the
class boot_out, which is a list of R lists,
each with three elements: est, implied_stats,
and ok.
This is the content of est of the first list:
boot_out_lavaan[[1]]$est
#> lhs op rhs est
#> 1 m ~ x 0.828
#> 2 m ~ c1 0.224
#> 3 m ~ c2 -0.231
#> 4 y ~ m 1.257
#> 5 y ~ x 0.089
#> 6 y ~ c1 -0.118
#> 7 y ~ c2 -0.632
#> 8 m ~~ m 0.571
#> 9 y ~~ y 4.317
#> 10 x ~~ x 1.207
#> 11 x ~~ c1 0.146
#> 12 x ~~ c2 0.115
#> 13 c1 ~~ c1 1.331
#> 14 c1 ~~ c2 0.153
#> 15 c2 ~~ c2 0.688The content is just the first four columns of the output of
lavaan::parameterEstimates(). Note that only fixed and free
parameters are used so other rows, if any, are not used even if
present.
This is the content of implied_stats of the first
list:
boot_out_lavaan[[1]]$implied_stats
#> $cov
#> m y x c1 c2
#> m 1.497
#> y 1.944 7.150
#> x 1.006 1.281 1.207
#> c1 0.383 0.241 0.146 1.331
#> c2 -0.030 -0.480 0.115 0.153 0.688
#>
#> $mean
#> numeric(0)
#>
#> $mean_lv
#> numeric(0)It has three elements. cov is the implied variances and
covariances of all variables. If a model has latent variables, they will
be included too. The other elements, mean and
mean_lv, are the implied means of the observed variables
and the latent variables (if any), respectively. They are of zero length
if mean structure is not in the fitted model.
The last element, ok, denotes whether the solution in a
bootstrap sample is admissible or not (determined by
lavaan::lavInspect() with
what = "post.check"). If not admissible, it will not be
used in forming confidence intervals.
Models Fitted by lm()
The output of do_boot() using the outputs of
lm() is identical to that using the output of
lavaan::sem(). It is an object of the class
boot_out, which is a list of R lists, each
with two elements: est and implied_stats.
This is the content of est of the first list:
boot_out_lm[[1]]$est
#> lhs op rhs est
#> 1 m ~ x 0.9583396
#> 2 m ~ c1 0.2808811
#> 3 m ~ c2 -0.3040130
#> 4 m ~1 9.9351030
#> 5 y ~ m 0.3986059
#> 6 y ~ x 0.5626298
#> 7 y ~ c1 0.5010449
#> 8 y ~ c2 -0.3614863
#> 9 y ~1 11.7212742The content is similar in structure to the output of
lavaan::parameterEstimates(). However, the estimates are
the estimates based on lm().
This is the content of implied_stats of the first
list:
boot_out_lm[[1]]$implied_stats
#> $cov
#> x c1 c2 m y
#> x 1.03034065 0.04418569 0.01709202 0.9946310 0.9921266
#> c1 0.04418569 1.13244802 0.12743087 0.3216875 0.6744295
#> c2 0.01709202 0.12743087 0.68082701 -0.1548074 -0.2343517
#> m 0.99463099 0.32168750 -0.15480736 1.7489520 1.4738922
#> y 0.99212663 0.67442949 -0.23435172 1.4738922 5.4383227
#>
#> $mean
#> x c1 c2 m y
#> 9.848009 2.329366 5.065314 18.487194 23.967238It has two elements. cov is the variances and
covariances of all variables. Unlike the output based on
lavaan::sem(), the content is just the sample variances and
covariances of the variables in each bootstrap sample, generated using
cov(). The other element, mean, stores sample
means of all variables in each bootstrap sample.
Further Information
For further information on do_boot(), please refer to
its help page.
References
Cheung, S. F., & Cheung, S.-H. (2024). manymome: An R package for computing the indirect effects, conditional effects, and conditional indirect effects, standardized or unstandardized, and their bootstrap confidence intervals, in many (though not all) models. Behavior Research Methods, 56(5), 4862–4882. https://doi.org/10.3758/s13428-023-02224-z
Falk, C. F., & Biesanz, J. C. (2015). Inference and interval estimation methods for indirect effects with latent variable models. Structural Equation Modeling: A Multidisciplinary Journal, 22(1), 24–38. https://doi.org/10.1080/10705511.2014.935266
Hayes, A. F. (2022). Introduction to mediation, moderation, and conditional process analysis: A regression-based approach (Third Edition). The Guilford Press.
Tofighi, D., & Kelley, K. (2020). Indirect effects in sequential mediation models: Evaluating methods for hypothesis testing and confidence interval formation. Multivariate Behavioral Research, 55(2), 188–210. https://doi.org/10.1080/00273171.2019.1618545