Skip to contents

Quick Function: Serial Mediation with Latent Variables

2025-12-15

Source: vignettes/articles/template_q_med_lav_serial.Rmd
template_q_med_lav_serial.Rmd

Introduction

This and other “Quick Function” articles are examples of R code to determine the range of sample sizes for a target level of power or estimate the power for a specific scenario in typical mediation models using power4mome. Users can quickly adapt them for their scenarios. They are how-to guides and will not cover the technical details involved.

Prerequisite

These functions are wrappers to power4test() and n_region_from_power(). For simple scenarios, users do not need to know how to use these advanced functions, though knowledge about them can help customizing the search for the region. Further information on these functions can be found in Final Remarks

Scope

This file is for serial mediation models, and only use one function q_power_mediation_serial() from the package power4mome.

The Model

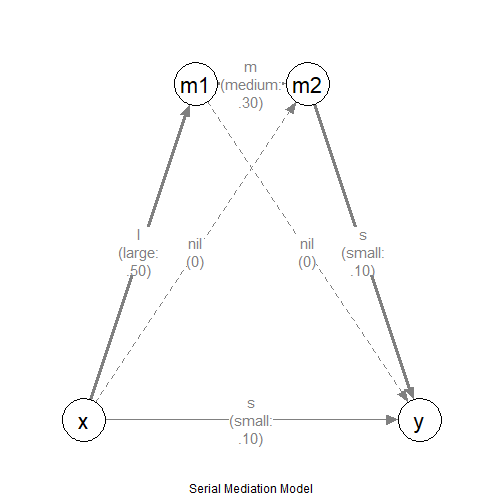
Suppose this is the model:

The Model

The Model

This is a serial mediation model, but the model is on the latent variables, each with some indicators.

We want to do power analysis for the indirect effect along the path x->m1->m2->y. Suppose these are the expected effects:

  • x->m1: medium

  • m1->m2: medium

  • m2->y: large

  • x->y: small

The other paths involving the mediators, x->m2 and m1->y, are assumed to have no effect (nil).

Convention for the Effect Sizes

To make it easy to specify the standardized population values of parameters, power4mome adopted the convention for Pearson’s r, just for convenience.

  • "nil": Nil (.00).

  • "s": Small (.10).

  • "m": Medium (.30),

  • "l": Large (.50).

There are also two intermediate levels:

  • "sm": Small-to-medium (.20).

  • "ml": Medium-to-large (.40).

If the effect is negative, just add a minus sign. For example, use "-m" to denote a negative medium effect.

For a path from one variable to another variable, the standardized coefficient is equal to the correlation if there are not other predictor, or if this predictor is uncorrelated with all other predictors. Therefore, though may not be perfect, we believe the convention of Pearson’s r is a reasonable one.

If necessary, users can specify the effect (on the standardized metric) directly.

Covariates in the Model to be Fitted

In applied research, the model to be fitted usually have other control variables, such as educational level. It may not be practical to specify all the probable effects of these control variables (though it is possible in power4mome).

Therefore, as a conservative assessment of power, users can first decide the population effects, and then adjust them slightly downward (e.g., from medium, "m", to small-to-medium, "sm") to take into account potential decrease in effects due to control variables to be included.

Model with Hypothesized Path Coefficients

This is the model with the effect sizes:

The Model

The Model

Test to be Used

In practice, nonparametric bootstrapping is usually used to test indirect effects. However, estimating its power using simulation is slow. A good-enough proxy is to estimate the power when testing this effect by Monte Carlo confidence interval. This is the default method in power4mome for tests of indirect effects.

Setting the Factor Loadings

One difficulty in doing power analysis for latent variable model is setting the population values for the indicators.

In power4mome, instead of setting factor loadings and error variances, users can specify the number of indicators and the population reliability of each latent factor. The corresponding factor loadings and error variances will be computed and specified automatically.

Therefore, when doing the power analysis, users can just specify the number of indicators (items) for each factor, which is usually known exactly or approximately in advance. The hypothesized population reliability coefficient may be based on previous studies or set to to a reasonable expectation (e.g., .70 for minimal acceptable reliability).

Find the Power

To estimate the power for a sample size, this is the code:

out_power <- q_power_mediation_serial(
  ab = c("m", "m", "l"),
  ab_other = "nil",
  cp = "s",
  number_of_indicators = c(x = 3,
                           m1 = 4,
                           m2 = 3,
                           y = 3),
  reliability = c(x = .70,
                  m1 = .80,
                  m2 = .70,
                  y = .70),
  target_power = .80,
  nrep = 400,
  n = 150,
  R = 1000,
  seed = 1234
)

These are the arguments:

  • ab: The hypothesized standardized effects along the path from the predictor x to the outcome variable y. This should be a character vector with elements equal to the number of mediators for the path coefficients x->m1->m2->...->y. Can be one of the labels supported by the convention, or a numeric value.

  • ab_other: The hypothesized standardized effect for all other paths involving the mediators. For simplicity, it only support one value, and this value will be used for all these paths. Can be one of the labels supported by the convention, or a numeric value.

  • cp: The hypothesized standardized direct effect from the predictor x to the outcome variable y. Can be one of the labels supported by the convention, or a numeric value.

  • number_of_indicators: A named numeric vector of the numbers of indicators. The names need to be x, m1, m2, … , and y. If it has only one value, then all latent variables have the same number of indicators.

  • reliability: A named numeric vector of the population reliability. The names need to be x, m1, m2, … , and y. If it has only one value, then all latent variables have the same value for reliability.

  • target_power: The target level of power. Default is .80, and can be omitted if this is the desired level of power

  • nrep: The number of replications when estimating the power for a sample size. Default is 400. Can be omitted if this is the desired number of replications.

  • R: The number of random samples used in forming Monte Carlo or nonparametric bootstrapping confidence intervals. Although they should be large when testing an effect in one single sample, they can be smaller because the goal is to estimate power across replications, not to achieve high accuracy in each sample. Default is 1000. Can be omitted if the default is acceptable.

  • seed: The seed for the random number generator. Note that, if parallel processing is used (this is the default), then the results are reproducible only if the configuration is exactly identical. Moreover, changes in the algorithm will also make results not reproducible even with the same seed. Nevertheless, it is still advised to set this seed to an integer, to make the results reproducible at least on the same machine.

This is the output:

out_power
#> 
#> ========== power4test Results ==========
#> 
#> 
#> ====================== Model Information ======================
#> 
#> == Model on Factors/Variables ==
#> m1 ~ x
#> m2 ~ m1 + x
#> y ~ m1 + m2 + x
#> == Model on Variables/Indicators ==
#> m1 ~ x
#> m2 ~ m1 + x
#> y ~ m1 + m2 + x
#> x =~ x1 + x2 + x3
#> m1 =~ m11 + m12 + m13 + m14
#> m2 =~ m21 + m22 + m23
#> y =~ y1 + y2 + y3
#> ====== Population Values ======
#> 
#> Regressions:
#>                    Population
#>   m1 ~                       
#>     x                 0.300  
#>   m2 ~                       
#>     m1                0.300  
#>     x                 0.000  
#>   y ~                        
#>     m1                0.000  
#>     m2                0.500  
#>     x                 0.100  
#> 
#> Variances:
#>                    Population
#>    .m1                0.910  
#>    .m2                0.910  
#>    .y                 0.731  
#>     x                 1.000  
#> 
#> (Computing indirect effects for 4 paths ...)
#> 
#> == Population Conditional/Indirect Effect(s) ==
#> 
#> == Indirect Effect(s) ==
#> 
#>                      ind
#> x -> m1 -> m2 -> y 0.045
#> x -> m1 -> y       0.000
#> x -> m2 -> y       0.000
#> x -> y             0.100
#> 
#>  - The 'ind' column shows the indirect effect(s).
#>  
#> ==== Population Reliability ====
#> 
#>    x  m1  m2   y
#>  0.7 0.8 0.7 0.7
#> 
#> == Population Standardized Loadings ==
#> 
#>      x    m1    m2     y
#>  0.661 0.707 0.661 0.661
#> ======================= Data Information =======================
#> 
#> Number of Replications:  400 
#> Sample Sizes:  150 
#> 
#> Call print with 'data_long = TRUE' for further information.
#> 
#> ==================== Extra Element(s) Found ====================
#> 
#> - fit
#> - mc_out
#> 
#> === Element(s) of the First Dataset ===
#> 
#> ============ <fit> ============
#> 
#> lavaan 0.6-21.2434 ended normally after 33 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        32
#> 
#>   Number of observations                           150
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                                55.395
#>   Degrees of freedom                                59
#>   P-value (Chi-square)                           0.609
#> 
#> =========== <mc_out> ===========
#> 
#> 
#> == A 'mc_out' class object ==
#> 
#> Number of Monte Carlo replications: 1000 
#> 
#> 
#> ====================== Test(s) Conducted ======================
#> 
#> - test_indirect: x->m1->m2->y
#> 
#> Call print() and set 'test_long = TRUE' for a detailed report.
#> 
#> ========== power4test Power ==========
#> 
#> [test]: test_indirect: x->m1->m2->y 
#> [test_label]: Test 
#>     est   p.v reject r.cilo r.cihi
#> 1 0.042 1.000  0.440  0.392  0.489
#> Notes:
#> - p.v: The proportion of valid replications.
#> - est: The mean of the estimates in a test across replications.
#> - reject: The proportion of 'significant' replications, that is, the
#>   rejection rate. If the null hypothesis is true, this is the Type I
#>   error rate. If the null hypothesis is false, this is the power.
#> - r.cilo,r.cihi: The confidence interval of the rejection rate, based
#>   on Wilson's (1927) method.
#> - Refer to the tests for the meanings of other columns.
#> 
#> ========== n_region_from_power Results ==========
#> 
#> 
#> 'mode' is not 'region' and results not available.

The first set of output is the default printout of the output of power4test(). This can be used to check the model specified. It also automatically computes the population standardized indirect effect(s).

The second section is the output of rejection_rates(), showing the power under the column reject.

In this example, the power is about 0.44 for sample size 150.

Find the Region of Sample Sizes

In addition to estimate the power for a sample size, the function can also be used to find an approximate region of sample sizes with levels of power not significantly different from the target power. This region is useful for determining a range of sample sizes likely to have sufficient power, but are not greater than necessary when resources are limited.

Note that this process can be slow. Nevertheless, power analysis is usually conducted in the planning stage of a study, and so the slow processing time is acceptable in this stage.

Finding the region can be done using the same code above, with the argument mode = "region" added:

out_region <- q_power_mediation_serial(
  ab = c("m", "m", "l"),
  ab_other = "nil",
  cp = "s",
  number_of_indicators = c(x = 3,
                           m1 = 4,
                           m2 = 3,
                           y = 3),
  reliability = c(x = .70,
                  m1 = .80,
                  m2 = .70,
                  y = .70),
  target_power = .80,
  nrep = 400,
  n = 150,
  R = 1000,
  seed = 1234,
  mode = "region"
)

This is the printout, showing only the section from the output of n_region_from_power():

#> ========== n_region_from_power Results ==========
#> 
#> Call:
#> n_region_from_power(object = `<hidden>`, target_power = 0.8, 
#>     progress = TRUE, simulation_progress = TRUE, max_trials = 10, 
#>     seed = 1234)
#> 
#>                      Setting                                      
#> Predictor(x)         Sample Size                                  
#> Goal:                Power significantly below or above the target
#> algorithm:           bisection                                    
#> Level of confidence: 95.00%                                       
#> Target Power:        0.800                                        
#> 
#> Solution: 
#> 
#> Approximate region of sample sizes with power:
#> - not significantly different from 0.800: 212 to 243
#> - significantly lower than 0.800: 212
#> - significantly higher than 0.800: 243
#> 
#> Confidence intervals of the estimated power:
#> - for the lower bound (212): [0.726, 0.809]
#> - for the upper bound (243): [0.817, 0.886]
#> 
#> Call `summary()` for detailed results.

In this example, the range of the sample size is 212 to 243.

The results can also be visualized using the plot() function:

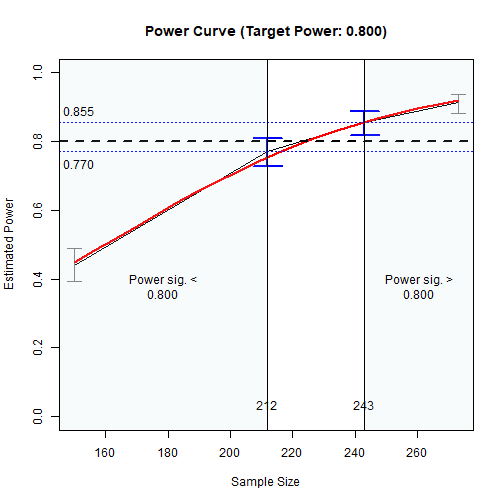
The Plot of Sample Sizes Searched

The Plot of Sample Sizes Searched

The region between the shaded areas is the approximate region of sample sizes found.

Final Remarks

Other Models

Quick how-to articles on other common mediation models, including those with latent variables, can be found from the list of articles

The package power4mome supports an arbitrary model specified by lavaan syntax, including those with moderators. Interested users can refer to the articles above.

Technical Details

For options of power4test() and n_region_from_power(), please refer to their help pages, as well as the Get-Started article and this article for n_from_power(), which is the function to find one of the regions, called twice by n_region_from_power().