
Standardized Case Influence on Parameter Estimates (Approximate)
Source:R/est_change_approx.R
est_change_approx.RdGets a lavaan::lavaan() output and computes the
approximate standardized changes in selected parameters for each case
if included.
Usage
est_change_approx(
fit,
parameters = NULL,
case_id = NULL,
allow_inadmissible = FALSE,
skip_all_checks = FALSE
)Arguments
- fit
The output from
lavaan::lavaan()or its wrappers (e.g.,lavaan::cfa()andlavaan::sem()).- parameters
A character vector to specify the selected parameters. Each parameter is named as in
lavaansyntax, e.g.,x ~ yorx ~~ y, as appeared in the columnslhs,op, andrhsin the output oflavaan::parameterEstimates(). Supports specifying an operator to select all parameters with these operators:~,~~,=~, and~1. This vector can contain both parameter names and operators. More details can be found in the help ofpars_id(). If omitted orNULL, the default, changes on all free parameters will be computed.- case_id
If it is a character vector of length equals to the number of cases (the number of rows in the data in
fit), then it is the vector of case identification values. If it isNULL, the default, thencase.idxused bylavaanfunctions will be used as case identification values.- allow_inadmissible
If
TRUE, accepts a fit object with inadmissible results (i.e.,post.checkfromlavaan::lavInspect()isFALSE). Default isFALSE.- skip_all_checks
If
TRUE, skips all checks and allows users to run this function on any object of thelavaanclass. For users to experiment this and other functions on models not officially supported. Default isFALSE.
Value
An est_change-class object, which is
matrix with the number of columns equals to the number of
requested parameters plus one, the last column being the
approximate generalized Cook's
distance. The number of rows equal to the number
of cases. The row names are the case identification values used in
lavaan_rerun(). The elements are approximate standardized
differences.
A print method is available for user-friendly output.
Details
For each case, est_change_approx() computes the
approximate differences in the estimates of selected parameters
with and without this case:
(Estimate with all case) - (Estimate without this case)
The differences are standardized by dividing the approximate raw differences by their standard errors. This is a measure of the standardized influence of a case on the parameter estimates if it is included.
If the value of a case is positive, including the case increases an estimate.
If the value of a case is negative, including the case decreases an estimate.
The model is not refitted. Therefore, the result is only an
approximation of that of est_change(). However, this
approximation is useful for identifying potentially influential
cases when the sample size is very large or the model takes a long
time to fit. This function can be used to identify potentially
influential cases quickly and then select them to conduct the
leave-one-out sensitivity analysis using lavaan_rerun() and
est_change().
This function also computes the approximate generalized Cook's
distance (gCD). To avoid confusion, it is labelled gcd_approx.
For the technical details, please refer to the vignette
on this approach: vignette("casewise_scores", package = "semfindr")
The approximate approach supports a model with equality constraints (available in 0.1.4.8 and later version).
Supports both single-group and multiple-group models. (Support for multiple-group models available in 0.1.4.8 and later version).
Author
Idea by Mark Hok Chio Lai https://orcid.org/0000-0002-9196-7406, implemented by Shu Fai Cheung https://orcid.org/0000-0002-9871-9448.
Examples
library(lavaan)
# A path model
dat <- pa_dat
mod <-
"
m1 ~ a1 * iv1 + a2 * iv2
dv ~ b * m1
a1b := a1 * b
a2b := a2 * b
"
# Fit the model
fit <- lavaan::sem(mod, dat)
summary(fit)
#> lavaan 0.6-19 ended normally after 1 iteration
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 5
#>
#> Number of observations 100
#>
#> Model Test User Model:
#>
#> Test statistic 6.711
#> Degrees of freedom 2
#> P-value (Chi-square) 0.035
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> m1 ~
#> iv1 (a1) 0.215 0.106 2.036 0.042
#> iv2 (a2) 0.522 0.099 5.253 0.000
#> dv ~
#> m1 (b) 0.517 0.106 4.895 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .m1 0.903 0.128 7.071 0.000
#> .dv 1.321 0.187 7.071 0.000
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> a1b 0.111 0.059 1.880 0.060
#> a2b 0.270 0.075 3.581 0.000
#>
# Approximate standardized changes and gCD
out_approx <- est_change_approx(fit)
head(out_approx)
#> m1~iv1 m1~iv2 dv~m1 m1~~m1 dv~~dv gcd_approx
#> 1 0.024713396 -0.030383580 0.052370026 -0.03784100 0.01630488 0.005850455
#> 2 0.007254736 0.003469647 -0.013223396 -0.06916983 -0.05953293 0.008312026
#> 3 -0.037982774 -0.039820283 -0.030150418 -0.06518369 -0.04609708 0.009904544
#> 4 -0.024353717 -0.003172373 0.021948305 -0.05277394 -0.04504791 0.005719499
#> 5 0.067010210 0.027951233 0.032981527 0.04860722 -0.06774242 0.012793226
#> 6 0.004065567 0.000983731 0.009640981 -0.07086163 -0.05565453 0.007984573
# Fit the model several times. Each time with one case removed.
# For illustration, do this only for the first 10 cases.
fit_rerun <- lavaan_rerun(fit, parallel = FALSE,
to_rerun = 1:10)
#> The expected CPU time is 0.45 second(s).
#> Could be faster if run in parallel.
# Compute the changes in chisq if a case is removed
out <- est_change(fit_rerun)
head(out)
#> a1 a2 b m1~~m1 dv~~dv gcd
#> 1 0.024466586 -0.0300705396 0.051965997 -0.03663071 0.01717427 0.005891665
#> 2 0.007153846 0.0034230301 -0.013043400 -0.06744802 -0.05802199 0.008147128
#> 3 -0.038282397 -0.0401051535 -0.029790144 -0.06335355 -0.04479763 0.009834826
#> 4 -0.024048244 -0.0031358865 0.021674577 -0.05137193 -0.04379632 0.005610493
#> 5 0.066686613 0.0278462201 0.032782898 0.04979077 -0.06598323 0.013001467
#> 6 0.004007056 0.0009699846 0.009509592 -0.06910195 -0.05422999 0.007823146
# Compare the results
plot(out_approx[1:10, 1], out[, 1])
abline(a = 0, b = 1)
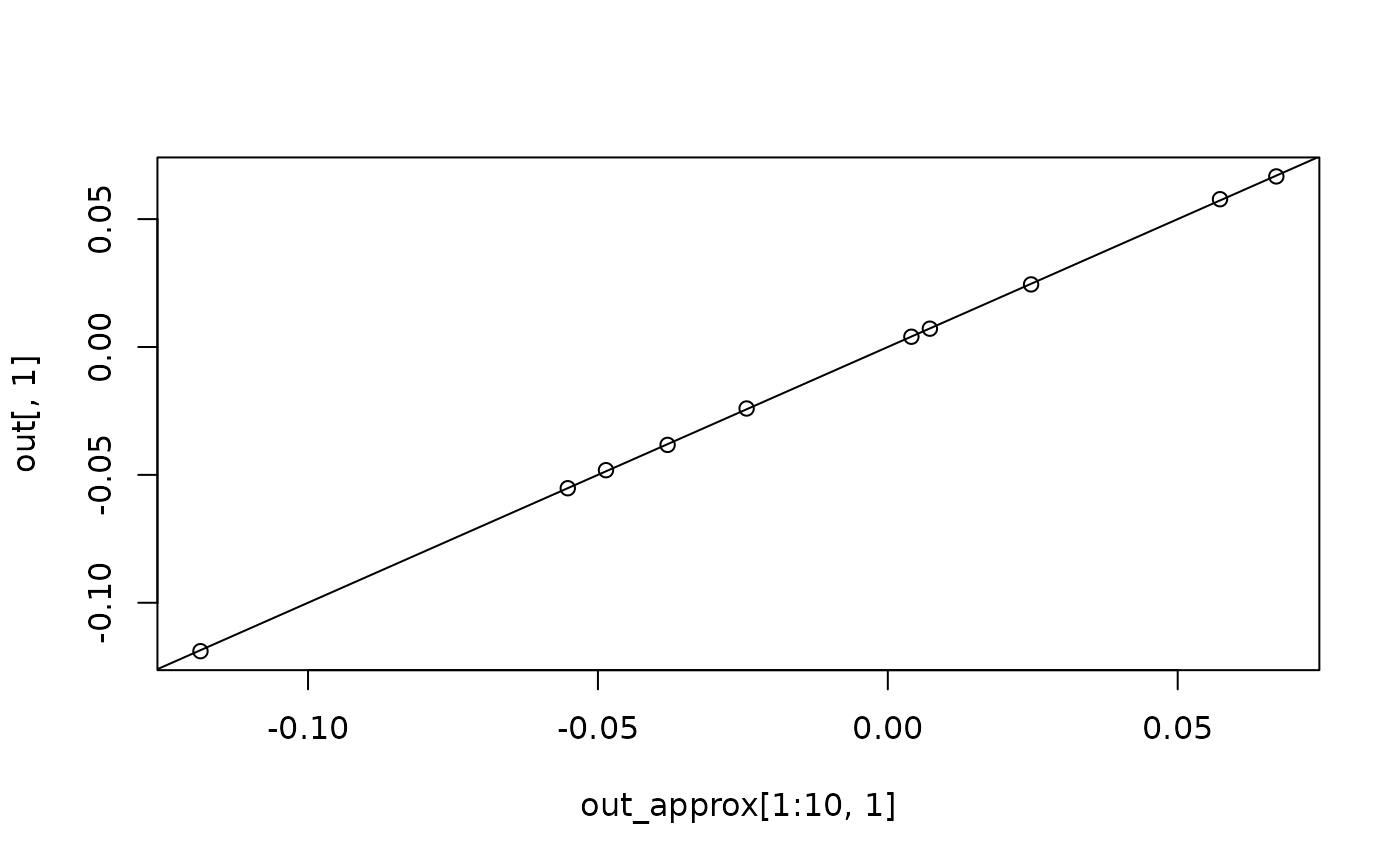 plot(out_approx[1:10, 2], out[, 2])
abline(a = 0, b = 1)
plot(out_approx[1:10, 2], out[, 2])
abline(a = 0, b = 1)
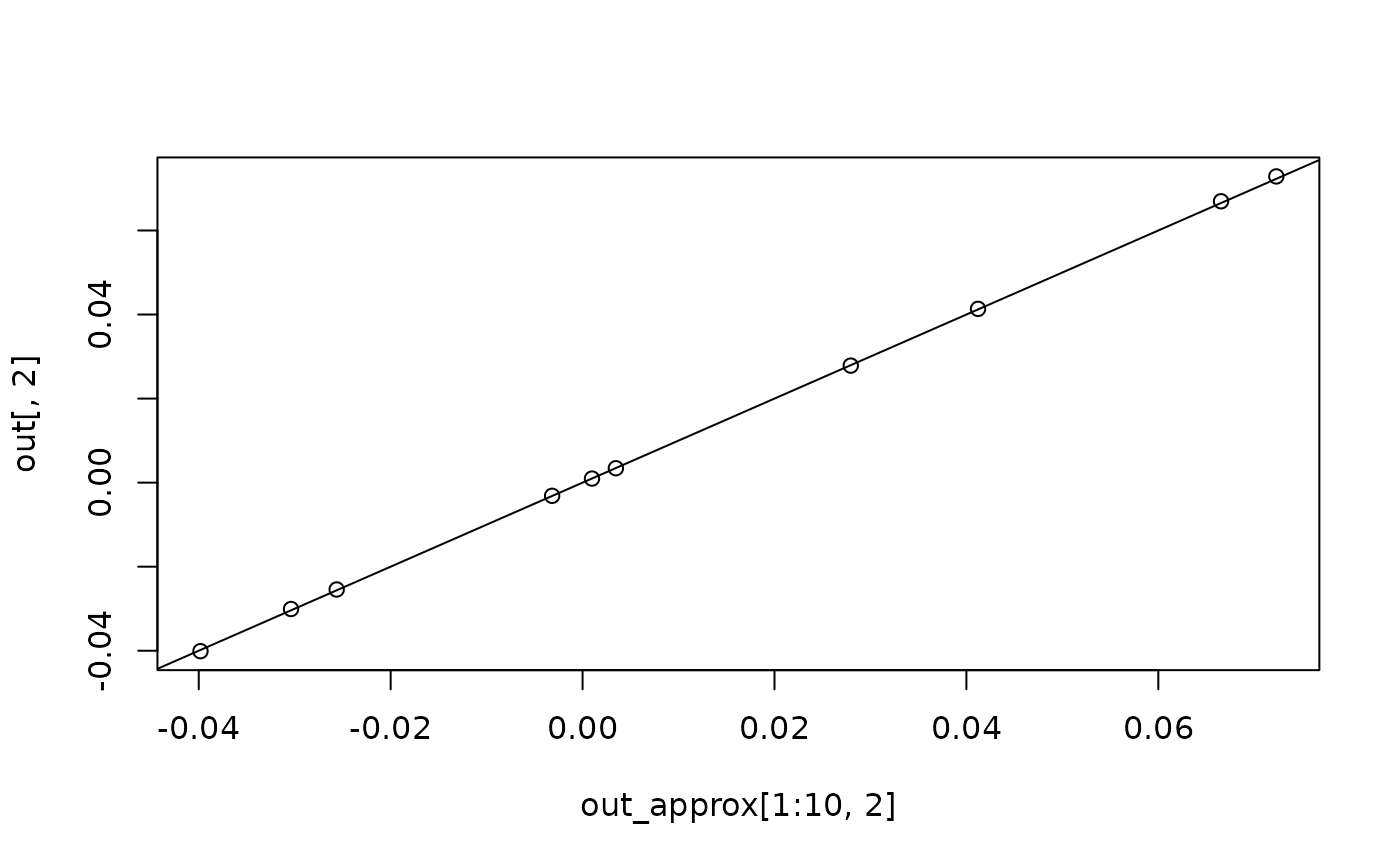 plot(out_approx[1:10, 3], out[, 3])
abline(a = 0, b = 1)
plot(out_approx[1:10, 3], out[, 3])
abline(a = 0, b = 1)
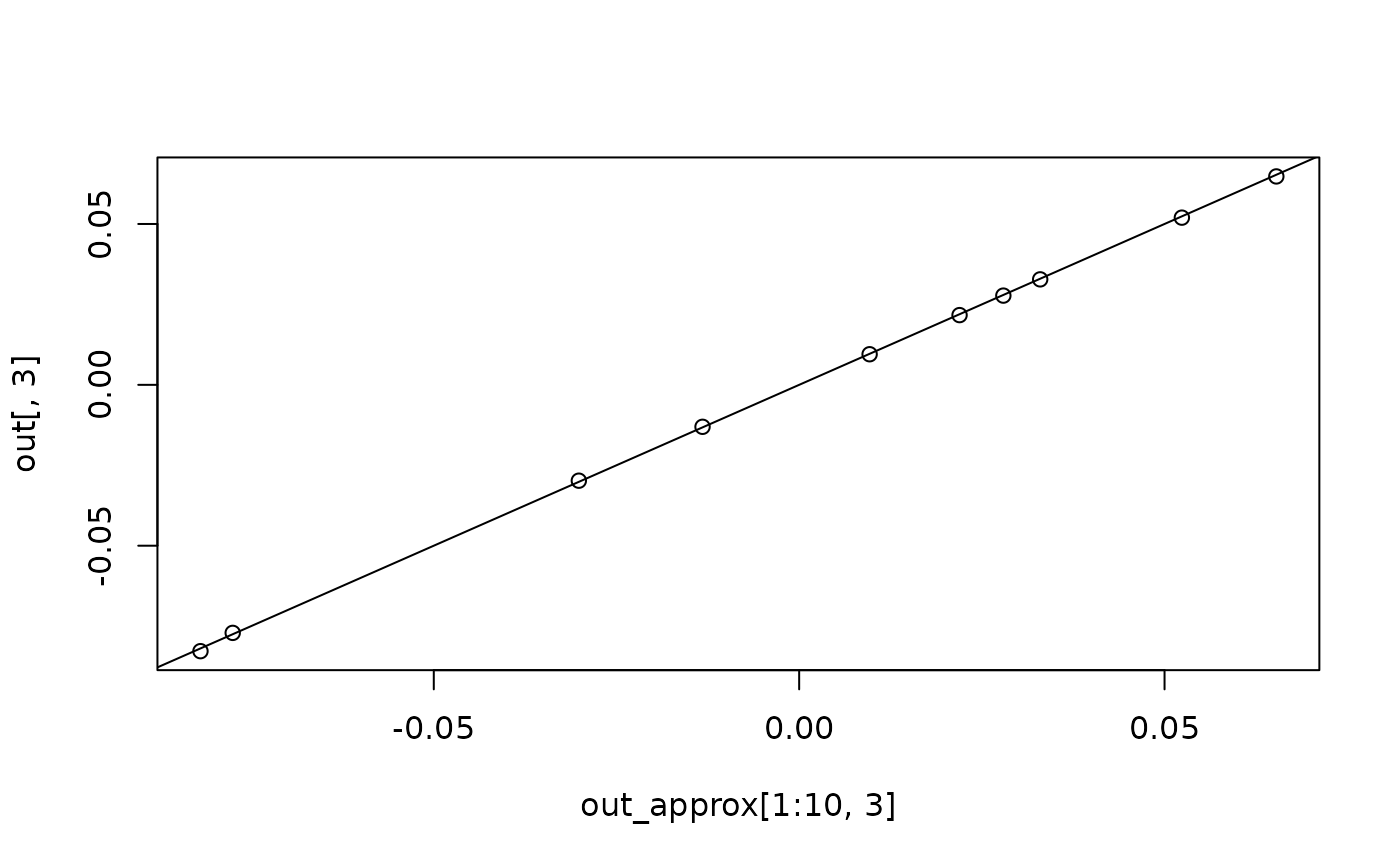 plot(out_approx[1:10, "gcd_approx"], out[, "gcd"])
abline(a = 0, b = 1)
plot(out_approx[1:10, "gcd_approx"], out[, "gcd"])
abline(a = 0, b = 1)
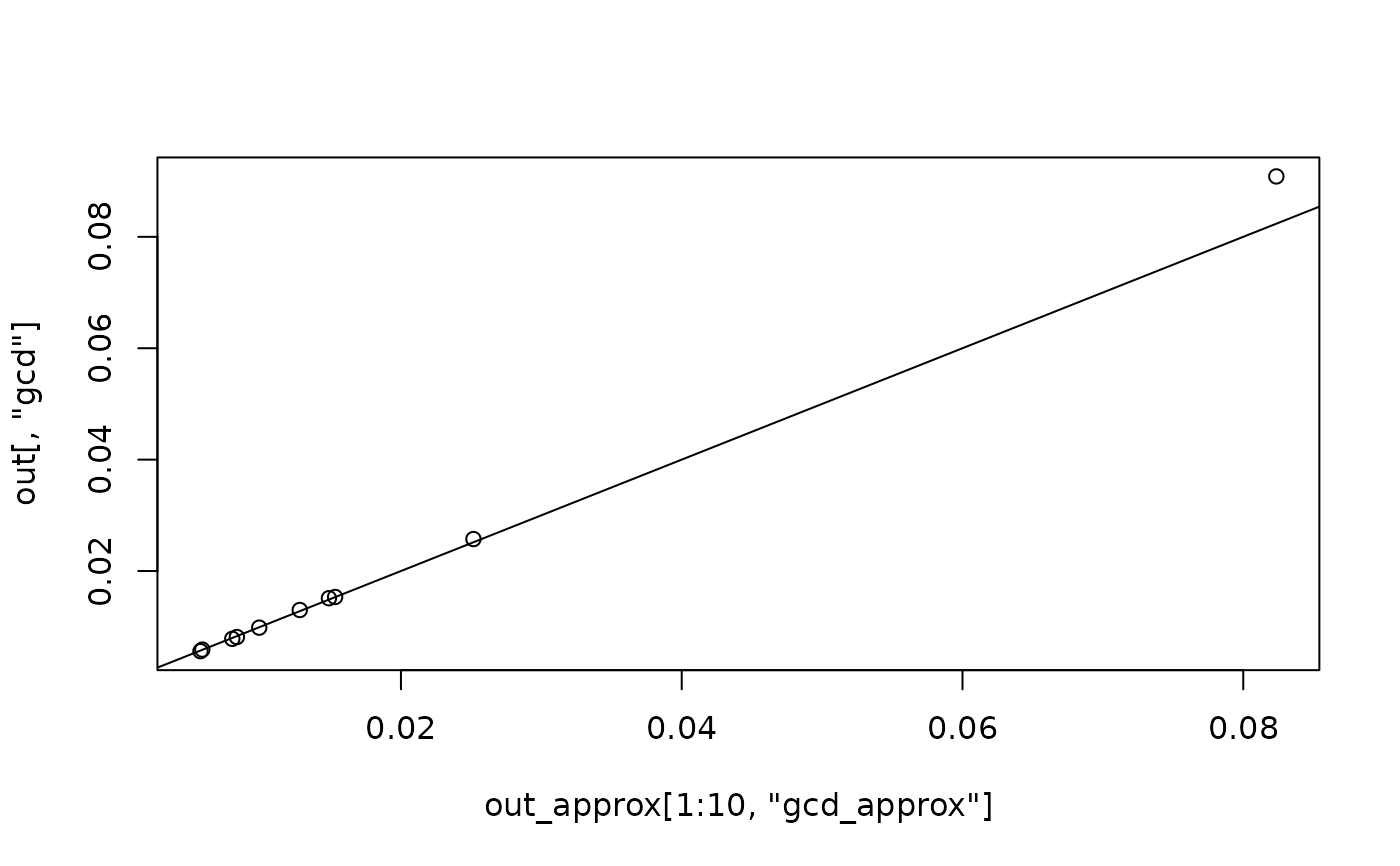 # A CFA model
dat <- cfa_dat
mod <-
"
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f1 ~~ f2
"
# Fit the model
fit <- lavaan::cfa(mod, dat)
summary(fit)
#> lavaan 0.6-19 ended normally after 37 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 13
#>
#> Number of observations 100
#>
#> Model Test User Model:
#>
#> Test statistic 12.027
#> Degrees of freedom 8
#> P-value (Chi-square) 0.150
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> f1 =~
#> x1 1.000
#> x2 0.767 0.225 3.405 0.001
#> x3 1.047 0.296 3.542 0.000
#> f2 =~
#> x4 1.000
#> x5 2.114 0.869 2.431 0.015
#> x6 0.992 0.377 2.635 0.008
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> f1 ~~
#> f2 0.171 0.091 1.884 0.060
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.841 0.221 3.802 0.000
#> .x2 1.214 0.208 5.823 0.000
#> .x3 1.018 0.251 4.064 0.000
#> .x4 1.103 0.186 5.918 0.000
#> .x5 0.993 0.437 2.270 0.023
#> .x6 0.882 0.158 5.575 0.000
#> f1 0.708 0.262 2.703 0.007
#> f2 0.250 0.151 1.659 0.097
#>
# Approximate standardized changes and gCD
# Compute gCD only for free loadings
out_approx <- est_change_approx(fit,
parameters = "=~")
head(out_approx)
#> f1=~x2 f1=~x3 f2=~x5 f2=~x6 gcd_approx
#> 1 0.00860861 0.03671007 0.0052771435 -0.0386456483 0.008701511
#> 2 0.26422237 0.25249192 0.0666230695 -0.1166435727 0.393874919
#> 3 -0.64655608 -0.01383399 -0.5070489021 -0.0291742969 3.185538515
#> 4 -0.04280393 -0.03874385 -0.0005649712 0.0060114092 0.007849339
#> 5 0.02203244 -0.07335966 0.0069759940 -0.0230738431 0.022193005
#> 6 0.01315800 0.06477736 -0.0193435883 0.0004489651 0.018492136
# A latent variable model
dat <- sem_dat
mod <-
"
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f3 =~ x7 + x8 + x9
f2 ~ a * f1
f3 ~ b * f2
ab := a * b
"
# Fit the model
fit <- lavaan::sem(mod, dat)
summary(fit)
#> lavaan 0.6-19 ended normally after 37 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 20
#>
#> Number of observations 200
#>
#> Model Test User Model:
#>
#> Test statistic 41.768
#> Degrees of freedom 25
#> P-value (Chi-square) 0.019
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> f1 =~
#> x1 1.000
#> x2 0.590 0.145 4.054 0.000
#> x3 0.808 0.168 4.812 0.000
#> f2 =~
#> x4 1.000
#> x5 0.730 0.099 7.400 0.000
#> x6 0.429 0.083 5.166 0.000
#> f3 =~
#> x7 1.000
#> x8 2.019 0.589 3.426 0.001
#> x9 2.747 0.788 3.486 0.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> f2 ~
#> f1 (a) 1.115 0.233 4.788 0.000
#> f3 ~
#> f2 (b) 0.206 0.061 3.394 0.001
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.183 0.173 6.831 0.000
#> .x2 1.129 0.127 8.909 0.000
#> .x3 1.027 0.134 7.667 0.000
#> .x4 0.833 0.173 4.812 0.000
#> .x5 1.078 0.140 7.714 0.000
#> .x6 1.234 0.132 9.367 0.000
#> .x7 1.056 0.112 9.428 0.000
#> .x8 1.042 0.139 7.478 0.000
#> .x9 1.077 0.197 5.470 0.000
#> f1 0.658 0.190 3.474 0.001
#> .f2 0.647 0.215 3.010 0.003
#> .f3 0.062 0.035 1.771 0.077
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> ab 0.230 0.079 2.895 0.004
#>
# Approximate standardized changes and gCD
# Compute gCD only for structural paths
out_approx <- est_change_approx(fit,
parameters = "~")
head(out_approx)
#> f2~f1 f3~f2 gcd_approx
#> 1 -0.004699340 -0.129875652 0.090920570
#> 2 0.047349346 -0.091081341 0.043044949
#> 3 -0.135088160 -0.090719323 0.136100353
#> 4 0.260922754 0.003871945 0.249947419
#> 5 -0.064745123 -0.016081058 0.018835545
#> 6 -0.009180409 -0.015223815 0.001833637
# A CFA model
dat <- cfa_dat
mod <-
"
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f1 ~~ f2
"
# Fit the model
fit <- lavaan::cfa(mod, dat)
summary(fit)
#> lavaan 0.6-19 ended normally after 37 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 13
#>
#> Number of observations 100
#>
#> Model Test User Model:
#>
#> Test statistic 12.027
#> Degrees of freedom 8
#> P-value (Chi-square) 0.150
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> f1 =~
#> x1 1.000
#> x2 0.767 0.225 3.405 0.001
#> x3 1.047 0.296 3.542 0.000
#> f2 =~
#> x4 1.000
#> x5 2.114 0.869 2.431 0.015
#> x6 0.992 0.377 2.635 0.008
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> f1 ~~
#> f2 0.171 0.091 1.884 0.060
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 0.841 0.221 3.802 0.000
#> .x2 1.214 0.208 5.823 0.000
#> .x3 1.018 0.251 4.064 0.000
#> .x4 1.103 0.186 5.918 0.000
#> .x5 0.993 0.437 2.270 0.023
#> .x6 0.882 0.158 5.575 0.000
#> f1 0.708 0.262 2.703 0.007
#> f2 0.250 0.151 1.659 0.097
#>
# Approximate standardized changes and gCD
# Compute gCD only for free loadings
out_approx <- est_change_approx(fit,
parameters = "=~")
head(out_approx)
#> f1=~x2 f1=~x3 f2=~x5 f2=~x6 gcd_approx
#> 1 0.00860861 0.03671007 0.0052771435 -0.0386456483 0.008701511
#> 2 0.26422237 0.25249192 0.0666230695 -0.1166435727 0.393874919
#> 3 -0.64655608 -0.01383399 -0.5070489021 -0.0291742969 3.185538515
#> 4 -0.04280393 -0.03874385 -0.0005649712 0.0060114092 0.007849339
#> 5 0.02203244 -0.07335966 0.0069759940 -0.0230738431 0.022193005
#> 6 0.01315800 0.06477736 -0.0193435883 0.0004489651 0.018492136
# A latent variable model
dat <- sem_dat
mod <-
"
f1 =~ x1 + x2 + x3
f2 =~ x4 + x5 + x6
f3 =~ x7 + x8 + x9
f2 ~ a * f1
f3 ~ b * f2
ab := a * b
"
# Fit the model
fit <- lavaan::sem(mod, dat)
summary(fit)
#> lavaan 0.6-19 ended normally after 37 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 20
#>
#> Number of observations 200
#>
#> Model Test User Model:
#>
#> Test statistic 41.768
#> Degrees of freedom 25
#> P-value (Chi-square) 0.019
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|)
#> f1 =~
#> x1 1.000
#> x2 0.590 0.145 4.054 0.000
#> x3 0.808 0.168 4.812 0.000
#> f2 =~
#> x4 1.000
#> x5 0.730 0.099 7.400 0.000
#> x6 0.429 0.083 5.166 0.000
#> f3 =~
#> x7 1.000
#> x8 2.019 0.589 3.426 0.001
#> x9 2.747 0.788 3.486 0.000
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> f2 ~
#> f1 (a) 1.115 0.233 4.788 0.000
#> f3 ~
#> f2 (b) 0.206 0.061 3.394 0.001
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .x1 1.183 0.173 6.831 0.000
#> .x2 1.129 0.127 8.909 0.000
#> .x3 1.027 0.134 7.667 0.000
#> .x4 0.833 0.173 4.812 0.000
#> .x5 1.078 0.140 7.714 0.000
#> .x6 1.234 0.132 9.367 0.000
#> .x7 1.056 0.112 9.428 0.000
#> .x8 1.042 0.139 7.478 0.000
#> .x9 1.077 0.197 5.470 0.000
#> f1 0.658 0.190 3.474 0.001
#> .f2 0.647 0.215 3.010 0.003
#> .f3 0.062 0.035 1.771 0.077
#>
#> Defined Parameters:
#> Estimate Std.Err z-value P(>|z|)
#> ab 0.230 0.079 2.895 0.004
#>
# Approximate standardized changes and gCD
# Compute gCD only for structural paths
out_approx <- est_change_approx(fit,
parameters = "~")
head(out_approx)
#> f2~f1 f3~f2 gcd_approx
#> 1 -0.004699340 -0.129875652 0.090920570
#> 2 0.047349346 -0.091081341 0.043044949
#> 3 -0.135088160 -0.090719323 0.136100353
#> 4 0.260922754 0.003871945 0.249947419
#> 5 -0.064745123 -0.016081058 0.018835545
#> 6 -0.009180409 -0.015223815 0.001833637